题目内容
关于空间两条直线 、
、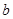 与平面
与平面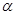 ,下列命题正确的是( )
,下列命题正确的是( )
 、
、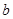 与平面
与平面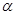 ,下列命题正确的是( )
,下列命题正确的是( )A.若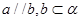 ,则 ,则 | B.若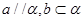 ,则 ,则 |
C.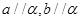 ,则 ,则 | D.若 则 则 |
D
试题分析:A:
 或
或 ,A错;B:
,A错;B: ,或
,或 异面,B错;C:
异面,B错;C: 或
或 或
或 异面,C错;
异面,C错;D:面面垂直的性质,D正确.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
题目内容
 、
、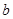 与平面
与平面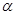 ,下列命题正确的是( )
,下列命题正确的是( )A.若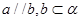 ,则 ,则 | B.若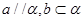 ,则 ,则 |
C.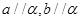 ,则 ,则 | D.若 则 则 |
 或
或 ,A错;B:
,A错;B: ,或
,或 异面,B错;C:
异面,B错;C: 或
或 或
或 异面,C错;
异面,C错;
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案