题目内容
18.求函数f(x)=$\frac{2x}{x+1}$,x∈(1,2]的值域.分析 通过分离常数可将原函数变成f(x)=$2-\frac{2}{x+1}$,而根据单调性的定义即可判断出f(x)在区间(1,2]上单调递增,从而其值域便可求得为(f(1),f(2)]=(1,$\frac{4}{3}$].
解答 解:f(x)=$\frac{2(x+1)-2}{x+1}=2-\frac{2}{x+1}$;
x增大时,$\frac{2}{x+1}$减小,-$\frac{2}{x+1}$增大,所以f(x)增大;
∴函数f(x)在(1,2]上单调递增;
∴$f(x)∈(f(1),f(2)]=(1,\frac{4}{3}]$;
∴函数f(x)在x∈(1,2]上的值域为(1,$\frac{4}{3}$].
点评 考查通过分离常数化简函数解析式的方法,根据函数的单调性定义判断函数的单调性,以及根据函数的单调性求其值域.

练习册系列答案
相关题目
11.已知直线l的斜率为2,M、N是直线l与双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1(a>0,b>0)$的两个交点,设M、N的中点为P(2,1),则C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{2}$ |
10.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{36}$=1(a>0)的顶点到渐近线的距离为2,则该双曲线的离心率为( )
| A. | 3 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{2}$ |
13.设函数f(x)满足2f′(x)>f(x),则一定成立的是( )
| A. | 3f(2ln2)<2f(2ln3) | B. | 3f(2ln2)>2f(2ln3) | C. | 2f(3ln3)<3f(2ln2) | D. | 2f(3ln3)>3f(2ln2) |
 与纵轴及直线
与纵轴及直线 所围成的封闭图形为区域
所围成的封闭图形为区域 ,不等式组
,不等式组 所确定的区域为
所确定的区域为 ,在区域
,在区域 内随机取一点,该点恰好在区域
内随机取一点,该点恰好在区域 的概率为( )
的概率为( ) B.
B. C.
C. D. 以上答案均不正确
D. 以上答案均不正确 的前
的前 项和为
项和为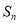 ,若
,若 ,且
,且 ,则
,则 等于( )
等于( )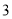 B.
B.  C.
C.  D.
D. 