题目内容
【题目】(改编)已知数列![]() 满足
满足![]() ,
, ![]() ,
, ![]() .
.
(1)若![]() ,
, ![]() ,
, ![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)设数列![]() 满足:
满足: ![]() ,
, ![]() ,设
,设![]() ,若
,若![]() ,
, ![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若![]() 成公比
成公比![]() 的等比数列,且
的等比数列,且![]() ,求正整数
,求正整数![]() 的最大值,以及
的最大值,以及![]() 取最大值时相应数列
取最大值时相应数列![]() 的公比
的公比![]() .
.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() 的最大值为1999,此时公比
的最大值为1999,此时公比 .
.
【解析】试题分析:(1)依题意得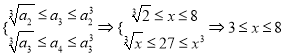 ;(2)令
;(2)令![]() ,则问题转化为:
,则问题转化为: ![]() 是公比为
是公比为![]() 的等比数列,
的等比数列, ![]()
![]() ,然后利用分类讨论思想求得
,然后利用分类讨论思想求得![]() ;(3)令
;(3)令![]()
![]()
当![]() 时,
时, ![]()
![]() 的最大值为
的最大值为![]() 此时
此时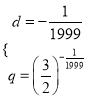 .
.
试题解析:
(1)依题意, ![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() ,综上可得:
,综上可得: ![]() ;
;
(2)令![]() ,则问题转化为:
,则问题转化为: ![]() 是公比为
是公比为![]() 的等比数列,
的等比数列, ![]() ,
,
设![]() ,若
,若![]() ,求
,求![]() 的范围.
的范围.
由已知得: ![]() ,又
,又![]() ,∴
,∴![]()
当![]() 时,
时, ![]() ,
, ![]() ,即
,即![]() ,成立
,成立
当![]() 时,
时, ![]() ,
, ![]() ,即
,即![]() ,
,
∴![]() ,此不等式即
,此不等式即![]() ,∵
,∵![]() ,
,
∴![]() ,
,
对于不等式![]() ,令
,令![]() ,得
,得![]() ,解得
,解得![]() ,
,
又当![]() 时,
时, ![]() ,
,
∴![]() 成立,
成立,
∴![]()
当![]() 时,
时, ![]() ,
, ![]() ,即
,即![]()
即![]() ,
, ![]() ,
, ![]() ,
,
∵![]()
![]()
∴![]() 时,不等式恒成立,综上,
时,不等式恒成立,综上, ![]() 的取值范围为
的取值范围为![]() .
.
(3)令![]() ,则
,则![]() 是首项为1,公差为
是首项为1,公差为![]() 的等差数列,
的等差数列,
满足![]() ,显然,当
,显然,当![]() ,
, ![]() 时,是一组符合题意的解,
时,是一组符合题意的解,
∴![]() ,则由已知得:
,则由已知得: ![]()
∴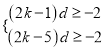 ,当
,当![]() 时,不等式即
时,不等式即![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() 时,
时, ![]() ,
,
解得![]() ,∴
,∴![]() ,
,
∴![]() 的最大值为1999,此时公差
的最大值为1999,此时公差![]() ,
,
此时公比 .
.

练习册系列答案
相关题目