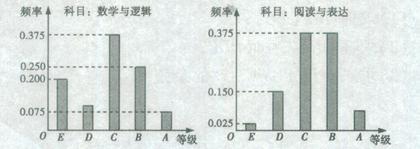
题目内容
为了估计某产品寿命的分布,对产品进行追踪调查,记录如下:
| 寿命(h) | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
| 个数 | 20 | 30 | 80 | 40 | 30 |
画出频率分布直方图;(2)估计产品在200~500以内的频率.
(1)见解析; (2)0.75
解析试题分析:(1)画频率分布直方图的步骤为:①确定组距和组数;②计算每组的频数和频率;③将频率和组距的比值计算出来并作为纵坐标(或将频率直接作为纵坐标);④画图.(2)将 内的频率加起来即可.
内的频率加起来即可.
试题解析:
由于频数和组距,组数都已弄出,可直接画图:
(2)估计产品在200~500以内的频率: .
.
考点:(1)频率分布直方图;(2)频率计算.

练习册系列答案
相关题目
某汽车厂生产的A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆)
| | 轿车A | 轿车B | 轿车C |
| 舒适性 | 800 | 450 | 200 |
| 标准型 | 100 | 150 | 300 |
(Ⅰ)在这个月生产的轿车中,用分层抽样的方法抽取n辆,其中有A类轿车45辆,求n的值;
(Ⅱ)在C类轿车中,用分层抽样的方法抽取一个容量为5的样本,将该样本看成一个总体,从中任取2辆,求至少1辆舒适型轿车的概率;
(Ⅲ)用随机抽样的方法从A类舒适型轿车中抽取10辆,经检测它们的得分如下:,8.7,9.3,8.2,9.4,8.6,9.2,9.6,9.0,8.4,8.6,把这10辆轿车的得分看作一个总体,从中任取一个数,求该数与总体平均数之差的绝对值超过0.6的概率.
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数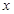 (个) (个) | 2 | 3 | 4 | 5 |
加工的时间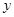 (小时) (小时) | 2.5 | 3 | 4 | 4.5 |
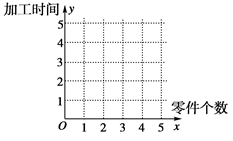
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出
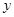 关于
关于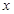 的线性回归方程
的线性回归方程 ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;(3)试预测加工
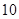 个零件需要多少时间?
个零件需要多少时间?参考公式:回归直线
 ,其中
,其中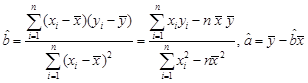 .
.
为调查某市老年人是否需要志愿者提供帮助,用简单随机抽样方法从该市调查了500位老年人,结果如右表.
| 性别 是否需要志愿者 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
(1)估计该市老年人中, 需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该市的老年人是否需要志愿者提供帮助与性别有关?
附:
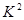
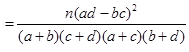 (
(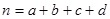 )
)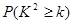 | 0.050 | 0.010 | 0.001 |
 | 3.841 | 6.635 | 10.828 |
某商场为了了解毛衣的月销售量 (件)与月平均气温
(件)与月平均气温 之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
月平均气温 | 17 | 13 | 8 | 2 |
月销售量 (件) (件) | 24 | 33 | 40 | 55 |
 中的
中的 ≈
≈ ,气象部门预测下个月的平均气温约为
,气象部门预测下个月的平均气温约为 ,据此估计该商场下个月毛衣销售量约为________________件.
,据此估计该商场下个月毛衣销售量约为________________件.  表示该班两个学生的百米测试成绩,已知
表示该班两个学生的百米测试成绩,已知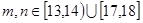 ,求事件
,求事件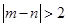 的概率.
的概率.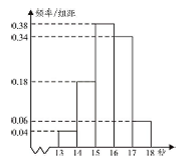
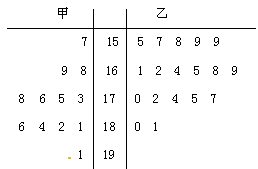
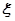 的分布列。
的分布列。