题目内容
我们把形如y=f(x)φ(x)的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边求对数得lny=φ(x)lnf(x),两边求导数,得
=φ′(x)lnf(x)+φ(x)
,于是y′=f(x)φ(x)[φ′(x)lnf(x)+φ(x)
],运用此方法可以探求得函数y=x
的一个单调递增区间是( )
| y′ |
| y |
| f′(x) |
| f(x) |
| f′(x) |
| f(x) |
| 1 |
| x |
分析:仔细分析题意,找出f(x),φ(x),然后依据题意求函数的导数,判断导数的单调性,求出单调增区间即可.
解答:解:仿照题目给定的方法,f(x)=x,φ(x)=
,
所以f′(x)=1,φ′(x)=-
,
由于y′=f(x)φ(x)[φ′(x)lnf(x)+φ(x)
],
所以y′=x
(-
lnx+
•
)=x
•
,
∵x>0,∴x
>0,x2>0,
∴要使y′>0,只要 1-lnx>0,解得:x∈(0,e)
故y=x
的一个单调递增区间为:(0,e),
故选:D.
| 1 |
| x |
所以f′(x)=1,φ′(x)=-
| 1 |
| x2 |
由于y′=f(x)φ(x)[φ′(x)lnf(x)+φ(x)
| f′(x) |
| f(x) |
所以y′=x
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1-lnx |
| x2 |
∵x>0,∴x
| 1 |
| x |
∴要使y′>0,只要 1-lnx>0,解得:x∈(0,e)
故y=x
| 1 |
| x |
故选:D.
点评:本题考查对数的运算性质,导数的运算,函数的单调性与导数的关系,考查计算能力,分析问题解决问题的能力,是基础题.

练习册系列答案
相关题目
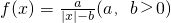 因其函数图象十分像汉字“囧”,故亲切称之为囧函数.现在为了方便讨论我们令a=b=1.
因其函数图象十分像汉字“囧”,故亲切称之为囧函数.现在为了方便讨论我们令a=b=1.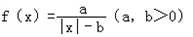 因其函数图象十分像汉字“囧”,故亲切称之为囧函数.现在为了方便讨论我们令a=b=1.
因其函数图象十分像汉字“囧”,故亲切称之为囧函数.现在为了方便讨论我们令a=b=1.