题目内容
已知椭圆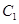 、抛物线
、抛物线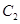 的焦点均在
的焦点均在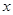 轴上,
轴上,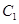 的中心和
的中心和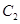 的顶点均为原点
的顶点均为原点 ,从每条曲线上取两个点,将其坐标记录如下:
,从每条曲线上取两个点,将其坐标记录如下: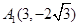 、
、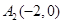 、
、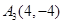 、
、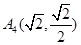 .
.
(1)经判断点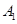 ,
,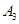 在抛物线
在抛物线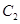 上,试求出
上,试求出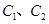 的标准方程;
的标准方程;
(2)求抛物线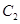 的焦点
的焦点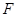 的坐标并求出椭圆
的坐标并求出椭圆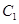 的离心率;
的离心率;
(3)过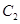 的焦点
的焦点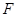 直线与椭圆
直线与椭圆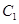 交不同两点
交不同两点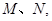 且满足
且满足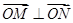 ,试求出直线的方程.
,试求出直线的方程.
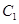 、抛物线
、抛物线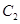 的焦点均在
的焦点均在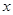 轴上,
轴上,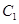 的中心和
的中心和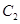 的顶点均为原点
的顶点均为原点 ,从每条曲线上取两个点,将其坐标记录如下:
,从每条曲线上取两个点,将其坐标记录如下: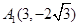 、
、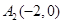 、
、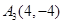 、
、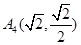 .
.(1)经判断点
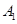 ,
,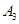 在抛物线
在抛物线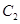 上,试求出
上,试求出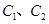 的标准方程;
的标准方程;(2)求抛物线
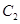 的焦点
的焦点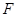 的坐标并求出椭圆
的坐标并求出椭圆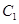 的离心率;
的离心率;(3)过
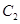 的焦点
的焦点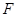 直线与椭圆
直线与椭圆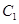 交不同两点
交不同两点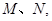 且满足
且满足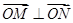 ,试求出直线的方程.
,试求出直线的方程.(1) ;(2)
;(2) ;(3)
;(3) 或
或 .
.
 ;(2)
;(2) ;(3)
;(3) 或
或 .
.试题分析:(1)先设抛物线
 ,然后将
,然后将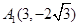 或
或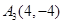 代入可得
代入可得 ,从而确定了
,从而确定了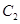 的方程,也进一步确定
的方程,也进一步确定 、
、 不在
不在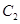 上,只能在
上,只能在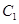 上;设
上;设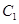 :
: ,把点
,把点 、
、 代入得
代入得 ,求解即可确定
,求解即可确定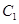 的方程;(2)由(1)中所求得的方程不难得到
的方程;(2)由(1)中所求得的方程不难得到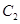 的焦点
的焦点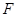 及椭圆
及椭圆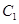 的离心率
的离心率 ;(3)先假设所求直线的方程
;(3)先假设所求直线的方程 (或
(或 ,不过此时要先验证直线斜率不存在的情况),然后联立直线与椭圆的方程,消去消去
,不过此时要先验证直线斜率不存在的情况),然后联立直线与椭圆的方程,消去消去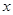 ,得
,得 ,得到
,得到 ,再得到
,再得到 ,要使
,要使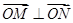 ,只须
,只须 ,从中求解即可得到
,从中求解即可得到 ,从而可确定直线的方程.
,从而可确定直线的方程.试题解析:(1)设抛物线
 ,则有
,则有 ,而
,而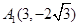 、
、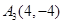 在抛物线上 2分
在抛物线上 2分将
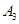 坐标代入曲线方程,得
坐标代入曲线方程,得 3分
3分设
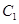 :
: ,把点
,把点 、
、 代入得
代入得 解得
解得
∴
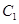 方程为
方程为 6分
6分(2)显然,
 ,所以抛物线焦点坐标为
,所以抛物线焦点坐标为
由(1)知,
 ,
,
所以椭圆的离心率为
 8分
8分(3)法一:直线过抛物线焦点
 ,设直线的方程为
,设直线的方程为 ,两交点坐标为
,两交点坐标为 ,
,由
 消去
消去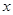 ,得
,得 10分
10分 ∴
 ①
①
 ② 12分
② 12分由
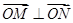 ,即
,即 ,得
,得
将①②代入(*)式,得
 ,解得
,解得 14分
14分所求的方程为:
 或
或 15分
15分法二:容易验证直线的斜率不存在时,不满足题意 9分
当直线斜率存在时,直线过抛物线焦点
 ,设其方程为
,设其方程为 ,与
,与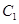 的交点坐标为
的交点坐标为
由
 消掉
消掉 ,得
,得 , 10分
, 10分于是
 ,
, ①
①
即
 ② 12分
② 12分由
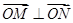 ,即
,即 ,得
,得
将①、②代入(*)式,得

解得
 14分
14分故所求的方程为
 或
或 15分.
15分.
练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 、
、 (
( )连线的斜率之积等于非零常数m的点的轨迹,加上
)连线的斜率之积等于非零常数m的点的轨迹,加上 、
、 两点所成的曲线C可以是圆、椭圆或双曲线.求曲线C的方程,并讨论C的形状与m值得关系.
两点所成的曲线C可以是圆、椭圆或双曲线.求曲线C的方程,并讨论C的形状与m值得关系.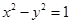 的焦点与椭圆
的焦点与椭圆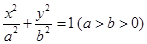 的焦点重合,且该椭圆的长轴长为
的焦点重合,且该椭圆的长轴长为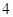 ,
,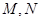 是椭圆上的的动点.
是椭圆上的的动点.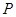 满足:
满足: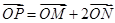 ,直线
,直线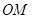 与
与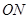 的斜率之积为
的斜率之积为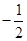 ,求证:存在定点
,求证:存在定点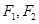 ,
,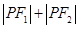 为定值,并求出
为定值,并求出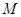 在第一象限,且点
在第一象限,且点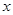 轴的射影为
轴的射影为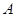 ,连接
,连接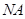 并延长交椭圆于
并延长交椭圆于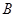 ,求证:以
,求证:以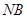 为直径的圆经过点
为直径的圆经过点 =1,过点M(2,0)且斜率不为0的直线交椭圆C于A,B两点.在x轴上若存在定点P,使PM平分∠APB,则P的坐标为________.
=1,过点M(2,0)且斜率不为0的直线交椭圆C于A,B两点.在x轴上若存在定点P,使PM平分∠APB,则P的坐标为________. +
+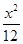 =1共焦点且过点(1,
=1共焦点且过点(1, )的双曲线的标准方程为( )
)的双曲线的标准方程为( ) =1
=1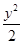 -
- =1
=1 上有一点P到左焦点的距离是4,则点p到右焦点的距离是( ).
上有一点P到左焦点的距离是4,则点p到右焦点的距离是( ).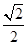 ,它的一个顶点为抛物线x2=4y的焦点.
,它的一个顶点为抛物线x2=4y的焦点.