题目内容
过点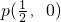
的直线l与直线x-y-1=0的交点在圆x2+y2=1上，则l的斜率为
- A.-2
- B.-2或0
- C.2
- D.2或0
D
分析：先联立x-y-1=0，x2+y2=1求出交点坐标，再由两点可求出直线l的斜率．
解答：联立x-y-1=0，x2+y2=1得到x2-x=0∴x=0或x=1
当x=0时，y=-1；当x=1时，y=0；
∴直线l与直线x-y-1=0的交点坐标为：（0，-1）或（1，0）
l的斜率k=
或k=
故选D．
点评：本题主要考查直线与圆相交的性质．考查直线与圆的位置关系的应用．高考中考查直线与圆的方程时一般以基础题为主，平时注意一些简单性质的应用和积累．
分析：先联立x-y-1=0，x2+y2=1求出交点坐标，再由两点可求出直线l的斜率．
解答：联立x-y-1=0，x2+y2=1得到x2-x=0∴x=0或x=1
当x=0时，y=-1；当x=1时，y=0；
∴直线l与直线x-y-1=0的交点坐标为：（0，-1）或（1，0）
l的斜率k=
或k=故选D．
点评：本题主要考查直线与圆相交的性质．考查直线与圆的位置关系的应用．高考中考查直线与圆的方程时一般以基础题为主，平时注意一些简单性质的应用和积累．
练习册系列答案
阅读快车系列答案
相关题目
（2006•朝阳区二模）如图，已知圆C：（x-1）2+y2=r2（r＞1），设M为圆C与x轴负半轴的交点，过M作圆C的弦MN，并使它的中点P恰好落在y轴上．
，点M在y轴上，且
，点C在x轴上移动．
的直线l与曲线E交于P，Q两点，设N(0，a)(a＜0)，
的夹角为
，求实数a的取值范围；
为半径的圆与曲线E在第一象限的交点为H，若圆在点H处的切线与曲线E在点H处的切线互相垂直，求实数m的值．
点M在y轴上，且
，点C在x轴上移动， （I）求点B的轨迹E的方程；（II）过点
的直线l与曲线E交于P、Q两点， 
的夹角为
为
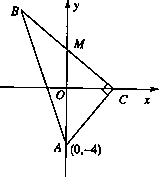
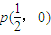的直线l与直线x-y-1=0的交点在圆x2+y2=1上，则l的斜率为（ ）