题目内容
【题目】已知原点![]() 到动直线
到动直线![]() 的距离为2,点
的距离为2,点![]() 到
到![]() ,
,![]() 的距离分别与
的距离分别与![]() 到直线
到直线![]() 的距离相等.
的距离相等.
(1)证明![]() 为定值,并求点
为定值,并求点![]() 的轨迹方程;
的轨迹方程;
(2)是否存在过点![]() 的直线
的直线![]() ,与
,与![]() 点的轨迹交于
点的轨迹交于![]() 两点,
两点,![]() 为线段
为线段![]() 的中点,且
的中点,且![]() ?若存在,请求出直线
?若存在,请求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(1)见解析,![]() .(2)见解析,
.(2)见解析,![]() 或
或![]() .
.
【解析】
(1)根据题意易证![]() 为定值,由
为定值,由![]() ,判定
,判定![]() 的轨迹为中心在原点,以
的轨迹为中心在原点,以![]() 为焦点的椭圆,根据椭圆定义可得椭圆方程;
为焦点的椭圆,根据椭圆定义可得椭圆方程;
(2)根据题意知直线![]() 的斜率存在,设出直线方程,与椭圆联立,由
的斜率存在,设出直线方程,与椭圆联立,由![]() 得出
得出![]() 的取值范围,再由
的取值范围,再由![]() 推得
推得![]() ,有韦达定理即可得出直线
,有韦达定理即可得出直线![]() 的方程.
的方程.
(1)设点![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() .
.
由已知,![]() ,
,![]() ,
,
又![]() 为
为![]() 的中点,
的中点,
![]() .
.
![]() 由椭圆定义可知,点
由椭圆定义可知,点![]() 的轨迹为中心在原点,以
的轨迹为中心在原点,以![]() 为焦点的椭圆.
为焦点的椭圆.
![]() ,
,![]() .
.![]() .
.
![]() 点
点![]() 的轨迹方程为
的轨迹方程为![]() .
.
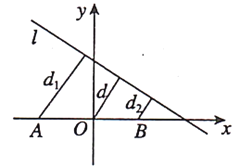
(2)假设直线![]() 存在,当
存在,当![]() 的斜率不存在时,显然
的斜率不存在时,显然![]() 不成立
不成立
![]() 设
设![]() ,
,![]() ,
,![]() .
.
由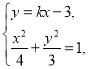 得
得![]()
![]() ,
,![]() 或
或![]() .
.
![]() ,
,![]() .
.
![]() ,
,
![]() .
.
![]() .
.
![]()
![]()
![]()
![]() .
.
![]() .
.
![]()
解得![]() 或
或![]() .
.
![]() ,且
,且![]() ,
,
![]() 存在直线
存在直线![]() 满足条件,直线
满足条件,直线![]() 的方程为
的方程为![]() 或
或![]() ,即
,即![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目