题目内容
【题目】已知函数f(x)=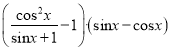 .
.
(l)求函数f(x)的定义域;
(2)求函数f(x)的值域.
【答案】(1){x∈R|x≠-![]() +2kπ,k∈Z}(2)
+2kπ,k∈Z}(2)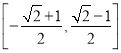
【解析】试题分析:(1)根据函数![]() 解析式,分母不为零,列出不等式求出解集即可求得函数
解析式,分母不为零,列出不等式求出解集即可求得函数![]() 的定义域;(2)利用二倍角的正弦公式、二倍角的余弦公式以及辅助角公式化简函数
的定义域;(2)利用二倍角的正弦公式、二倍角的余弦公式以及辅助角公式化简函数![]() 的解析式为一个角的三角函数形式,利用三角函数的有界性,即可求出
的解析式为一个角的三角函数形式,利用三角函数的有界性,即可求出![]() 的值域.
的值域.
试题解析:(1)由sinx+1≠0得,x≠-![]() +2kπ(k∈Z),
+2kπ(k∈Z),
∴f(x)的定义域为{x∈R|x≠![]() -+2kπ,k∈Z}.
-+2kπ,k∈Z}.
(2)f(x)=(![]() -1)(sinx-cosx)=(1-sinx-1)(sinx-cosx)
-1)(sinx-cosx)=(1-sinx-1)(sinx-cosx)
=-sinx(sinx-cosx)=sinxcosx-sin2x
=![]() sin2x-
sin2x-![]() = (sin2x+cos2x)
= (sin2x+cos2x) ![]()
=![]() sin(2x+
sin(2x+![]() )-
)-![]() {x|x≠-
{x|x≠-![]() +2kπ,k∈Z}
+2kπ,k∈Z}
虽然当x=-![]() +2kπ(k∈Z)时,f(x)=-1,但是
+2kπ(k∈Z)时,f(x)=-1,但是
f(x)=-1![]() {x|
{x| ![]() 或
或![]() ,k∈Z}
,k∈Z}![]() {x|x=-
{x|x=-![]() +2kπ,k∈Z}
+2kπ,k∈Z}
∴函数f(x)的值域为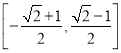

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目