题目内容
(文科做)函数①y=2(x-1)2-1,②y=x2-3|x|+4,③y= ,④y=
,④y= 中即非奇函数也非偶函数的是( )
中即非奇函数也非偶函数的是( )A.①②③
B.①③④
C.①③
D.①
【答案】分析:根据函数奇偶性的定义逐个判断即可得到答案.
解答:解:①y=2(x-1)2-1 的图象关于x=1对称,不关于y轴对称,也不关于原点对称,
所以y=2(x-1)2-1 既不是奇函数也不是偶函数;
②y=x2-3|x|+4 的定义域为R,关于原点对称,
y=x2-3|x|+4 且(-x)2-3|-x|+4=y=x2-3|x|+4,
所以y=x2-3|x|+4为偶函数;
③y= 的定义域为[0,+∞),不关于原点对称,
的定义域为[0,+∞),不关于原点对称,
所以y= 既非奇函数也非偶函数;
既非奇函数也非偶函数;
④y= 的定义域为{x|x≠0},关于原点对称,
的定义域为{x|x≠0},关于原点对称,
且 =-
=- ,为奇函数,
,为奇函数,
综上,既非奇函数也非偶函数的为①③.
故选C.
点评:本题考查函数奇偶性的判断,属基础题,利用定义、图象是判断函数奇偶性的基本方法.
解答:解:①y=2(x-1)2-1 的图象关于x=1对称,不关于y轴对称,也不关于原点对称,
所以y=2(x-1)2-1 既不是奇函数也不是偶函数;
②y=x2-3|x|+4 的定义域为R,关于原点对称,
y=x2-3|x|+4 且(-x)2-3|-x|+4=y=x2-3|x|+4,
所以y=x2-3|x|+4为偶函数;
③y=
 的定义域为[0,+∞),不关于原点对称,
的定义域为[0,+∞),不关于原点对称,所以y=
 既非奇函数也非偶函数;
既非奇函数也非偶函数;④y=
 的定义域为{x|x≠0},关于原点对称,
的定义域为{x|x≠0},关于原点对称,且
 =-
=- ,为奇函数,
,为奇函数,综上,既非奇函数也非偶函数的为①③.
故选C.
点评:本题考查函数奇偶性的判断,属基础题,利用定义、图象是判断函数奇偶性的基本方法.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 ,④y=
,④y=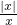 中即非奇函数也非偶函数的是
中即非奇函数也非偶函数的是 ,④y=
,④y= 中即非奇函数也非偶函数的是( )
中即非奇函数也非偶函数的是( )