题目内容
如图,三棱锥P-ABC中,已知PA^平面ABC, PA=3,PB=PC=BC="6," 求二面角P-BC-A的正弦值
解:取BC的中点D,连结PD,AD,∵ PB =PC,∴ PD⊥BC
∵ PA⊥平面ABC,由三垂线定理的逆定理得 AD⊥BC
∴ ∠PDA就是二面角P-BC-A的平面角
∵ PB = PC = BC =" 6" ,∴ PD =

sin∠PDA=
 即二面角P-BC-A的正弦值是
即二面角P-BC-A的正弦值是

解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
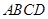 中,
中, ∥
∥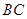 ,
,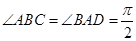 ,
,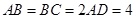 ,
,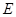 、
、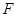 分别是
分别是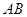 、
、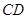 上的点,
上的点,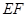 ∥
∥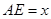 ,
,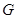 是
是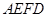 ⊥平面
⊥平面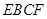 (如图).
(如图).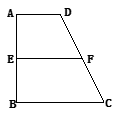
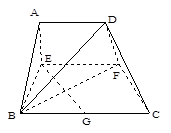
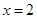 时,求证:
时,求证: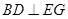 ;
;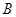 、
、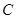 、
、 为顶点的三棱锥的体积记为
为顶点的三棱锥的体积记为 ,求
,求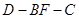 的余弦值.
的余弦值. 中,
中,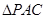 和
和 是边长为
是边长为 的等边三角形,
的等边三角形,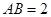 ,
, 分别是
分别是 的中点.
的中点.
 ∥平面
∥平面 ;
; ⊥平面
⊥平面 ;
;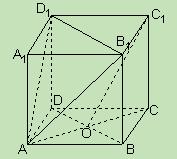

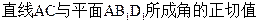
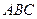 为底面的棱柱被平面
为底面的棱柱被平面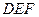 所截而得,已
所截而得,已 知
知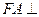 平面
平面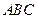 ,
, ,
, ,
,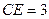 ,
,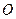 为
为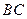 的中点,
的中点,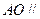 面
面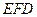 .
.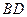 的长;
的长;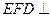 面
面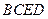 ;
;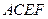 相交所成锐角二面角的余弦值.
相交所成锐角二面角的余弦值.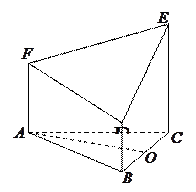
 =BC,PA=AB。
=BC,PA=AB。

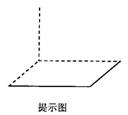
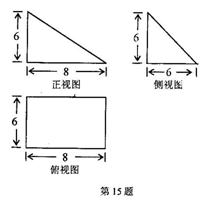
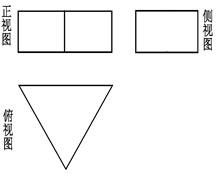
 图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:
图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位: )
) 图中连结
图中连结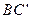 ,证明:
,证明: