题目内容
设函数f(x)=x2-2x+3,g(x)=x2-x
(1)解不等式|f(x)-g(x)|≥2 014;
(2)若|f(x)-a|<2恒成立的充分条件是1≤x≤2,求实数a的取值范围.
解:(1)由|f(x)-g(x)|≥2 012得|-x+3|≥2 012,即|x-3|≥2 011,所以x-3≥2 012或x-3≤-2 012,解得x≥2 015或x≤-2 009.
(2)依题意知:当1≤x≤2时,|f(x)-a|<2恒成立,所以当1≤x≤2时,-2<f(x)-a<2恒成立,即f(x)-2<a<f(x)+2恒成立.
由于当1≤x≤2时,f(x)=x2-2x+3=(x-1)2+2的最大值为3,最小值为2,因此3-2<a<2+2,即1<a<4,所以实数a的取值范围(1,4).

练习册系列答案
相关题目
 上一动点,PA,PB是圆C:
上一动点,PA,PB是圆C: 的两条切线,A.B是切点,若四边形PACB的最小面积是2,则
的两条切线,A.B是切点,若四边形PACB的最小面积是2,则 的值为 ( )
的值为 ( ) C.
C. D.2
D.2 ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 表示焦距为8的双曲线,则m 的值等于
表示焦距为8的双曲线,则m 的值等于  是曲线
是曲线 的切线,则
的切线,则 的值为
的值为 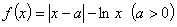 .
.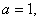 求
求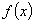 的单调区间及
的单调区间及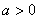 ,求
,求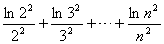 与
与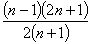 的大小.
的大小.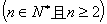 ,并证明你的结论.
,并证明你的结论. ,焦距为4,则该椭圆的方程为
,焦距为4,则该椭圆的方程为  B
B  +
+ =1 C
=1 C  +
+ =1 D
=1 D  的倾斜角为
的倾斜角为 ,集合
,集合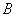 为函数
为函数 的定义域,则
的定义域,则 ( )
( )