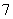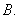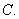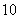题目内容
设函数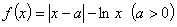 .
.
(1)若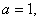 求
求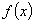 的单调区间及
的单调区间及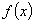 的最小值;
的最小值;
(2)若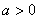 ,求
,求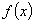 的单调区间;
的单调区间;
(3)试比较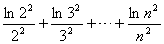 与
与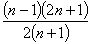 的大小.
的大小.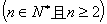 ,并证明你的结论.
,并证明你的结论.
解:(1)
当 时,
时,
 在区间
在区间 上是递增的.
上是递增的.
当 时,
时,
 在区间
在区间 上是递减的.
上是递减的.
故 时,
时,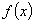 的增区间为
的增区间为 ,减区间为
,减区间为 ,
, .
.
(2)若 ,当
,当 时,
时,

则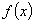 在区间
在区间 上是递增的;
上是递增的;
当 时,
时, ,
, 
 在区间
在区间 上是递减的.
上是递减的.
若 ,当
,当 时,
时,

则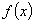 在区间
在区间 上是递增的,
上是递增的, 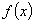 在区间
在区间 上是递减的;
上是递减的;
当 时,
时, ,
, 
 在区间
在区间 上是递减的,而
上是递减的,而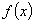 在
在 处有意义;
处有意义;
则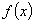 在区间
在区间 上是递增的,在区间
上是递增的,在区间 上是递减的.
上是递减的.
综上: 当 时,
时, 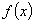 的递增区间是
的递增区间是 ,递减区间是
,递减区间是 ;
;
当 ,
,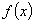 的递增区间是
的递增区间是 ,递减区间是
,递减区间是 . (3)由(1)可知,当
. (3)由(1)可知,当 时,有
时,有 即
即


= .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的展开式中各项系数的和为243,则该展开式中常数项为 .
的展开式中各项系数的和为243,则该展开式中常数项为 . 满足
满足 ,则
,则 ;
; ”的否定是 .
”的否定是 .
 ,现用分层抽样的方法从该校高中三个年级的学生中抽
,现用分层抽样的方法从该校高中三个年级的学生中抽 为直线,
为直线, 是两个不同的平面,下列命题中正确的是
是两个不同的平面,下列命题中正确的是 ,
, ,则
,则 B.若
B.若 ,
, ,则
,则 ,
,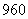 人中抽取
人中抽取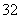 人做问卷调查,为此将他们随机编号为
人做问卷调查,为此将他们随机编号为 ,
,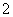 ,……,
,……,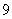 .抽到的
.抽到的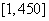 的人做问卷
的人做问卷 ,编号落入区间
,编号落入区间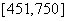 的人做问卷
的人做问卷 ,其余的人做问卷
,其余的人做问卷 .则抽到的人中,做问卷
.则抽到的人中,做问卷