题目内容
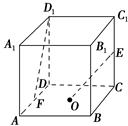
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点.那么异面直线OE和FD1所成的角的余弦值等于 ( ).

A. | B. | C. | D. |
D
建立如图所示的空间直角坐标系,则O(1,1,0),E(0,2,1),D1(0,0,2),F(1,0,0), =(-1,1,1),
=(-1,1,1), =(-1,0,2),∴
=(-1,0,2),∴ ·
· =3,|
=3,| |=
|= ,|
,| |=
|= ,
,

∴cos〈 ,
, 〉=
〉= =
= .
.
即OE与FD1所成的角的余弦值为 .
.
 =(-1,1,1),
=(-1,1,1), =(-1,0,2),∴
=(-1,0,2),∴ ·
· =3,|
=3,| |=
|= ,|
,| |=
|= ,
,
∴cos〈
 ,
, 〉=
〉= =
= .
.即OE与FD1所成的角的余弦值为
 .
.
练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
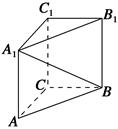
 中,
中,
 底面
底面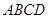 ,且底面
,且底面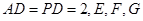 分别为
分别为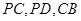 的中点.
的中点.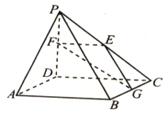
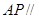 平面
平面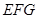 ;
;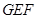 和平面
和平面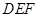 的夹角.
的夹角.  是边长为
是边长为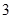 的正方形,
的正方形,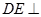 平面
平面 ,
,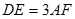 ,
,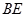 与平面
与平面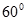 .
.
 平面
平面 ;
; 的余弦值;
的余弦值;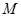 是线段
是线段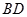 上一个动点,试确定点
上一个动点,试确定点 平面
平面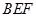 ,并证明你的结论.
,并证明你的结论.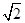 .
.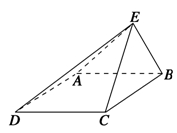
 外一点,A为平面
外一点,A为平面 为平面
为平面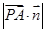
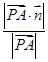
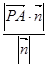
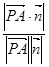
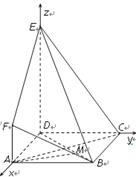
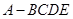 中,
中,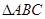 是正三角形,四边形
是正三角形,四边形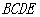 是矩形,且平面
是矩形,且平面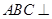 平面
平面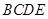 ,
,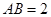 ,
,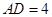 .
.
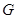 是
是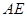 的中点,求证:
的中点,求证: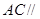 平面
平面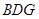 ;
; 为线段
为线段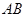 的中点,求二面角
的中点,求二面角 的正切值.
的正切值. (3,-2),
(3,-2), (-2,1),
(-2,1), (7,-4),若
(7,-4),若 ,则
,则 ,
, ______.
______.