Question

（1）在极坐标系（ρ，θ）（0≤θ＜2π）中，曲线ρ=2sinθ与ρcosθ=-1的交点的极坐标为

2 ， 3π 4

．
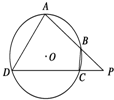
（2）如图，四边形ABCD是圆O的内接四边形，延长AB和DC相交于点P，若

PB

PA

=

1

2

，

PC

PD

=

1

3

，则

BC

AD

的值为

6

6

．

Answer 1

分析：（1）曲线ρ=2sinθ化为直角坐标方程x²+（y-1）²=1，而ρcosθ=-1化为直角坐标方程为x=-1．联立方程组求出交点的直角坐标，再化为极坐标．
由割线定理知：PB•PA=PC•PD，再由已知条件可得PB=

6

6

PD，再由△PBC∽△PDA，可得

BC

AD

=

PB

PD

．

解答：解：（1）曲线ρ=2sinθ化为直角坐标方程为x²+y²=2y，即x²+（y-1）²=1，
而ρcosθ=-1化为直角坐标方程为x=-1．
直线x=-1与圆x²+（y-1）²=1的交点坐标为（-1，1），化为极坐标为

2 ， 3π 4

．
（2）由割线定理知：PB•PA=PC•PD，
又∵PA=2PB，PD=3PC，∴PB•2PB=

1

3

PD•PD，∴PB²=

1

6

PD²，∴PB=

6

6

PD，
又∵△PBC∽△PDA，∴

BC

AD

=

PB

PD

=

6

6

．

点评：本题主要考查把极坐标方程化为直角坐标方程的方法，与圆有关的比例线段，属于基础题．