题目内容
 下面求2+5+8+11+…+2012的值的伪代码中,正整数m的最大值为
下面求2+5+8+11+…+2012的值的伪代码中,正整数m的最大值为2015
2015
.分析:根据已知中程序的功能,我们可以分析出累加项的步长为3,循环变量I的终值为2012,故2012<m<2016,进而可得m的最大值.
解答:解:由伪代码知,这是当型循环结构的算法,
由于累加项的步长为3,
循环变量I的终值为2012
故2012<m<2016
由于m是正整数,所以最大值为2015.
故答案为:2015
由于累加项的步长为3,
循环变量I的终值为2012
故2012<m<2016
由于m是正整数,所以最大值为2015.
故答案为:2015
点评:本题考查的知识点是伪代码,其中熟练掌握当型结构的特点,并根据已知中的程序功能分析出循环变量的终值,是解答的关键.

练习册系列答案
相关题目
(本小题满分12分)
从某校高三年级900名学生中随机抽取了 名测量身高,据测量被抽取的学生的身高全部介于
名测量身高,据测量被抽取的学生的身高全部介于 和
和 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组 ,第二组
,第二组 …第八组
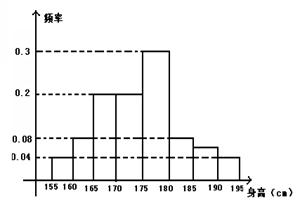
…第八组 ,右图是按上述分组方法得到的条形图.
,右图是按上述分组方法得到的条形图.
(1)根据已知条件填写下面表格:
|
组 别 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
样本数 |
|
|
|
|
|
|
|
|
(2)估计这所学校高三年级900名学生中,身高在 以上(含
以上(含 )的人数;
)的人数;
(3)在样本中,若第二组有 人为男生,其余为女生,第七组有
人为男生,其余为女生,第七组有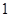 人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,用
人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,用 表示实验小组中男同学的人数,求
表示实验小组中男同学的人数,求 的分布列及期望
的分布列及期望
.
(本题满分12分)海水受日月的引力,在一定的时候发生涨落的现象叫潮,一般地,早潮叫潮,晚潮叫汐. 在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋. 下面是某港口在某季节每天的时间与水深关系表:
|
时刻 |
2:00 |
5:00 |
8:00 |
11:00 |
14:00 |
17:00 |
20:00 |
23:00 |
|
水深(米) |
7.5 |
5.0 |
2.5 |
5.0 |
7.5 |
5.0 |
2.5 |
5.0 |
经长期观测,这个港口的水深与时间的关系,可近似用函数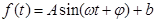
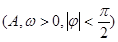 来描述.
来描述.
(1) 根据以上数据,求出函数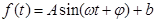 的表达式;
的表达式;
(2) 一条货船的吃水深度(船底与水面的距离)为4.25米,安全条例规定至少要有2米的安全间隙(船底与洋底的距离),该船在一天内(0:00~24:00)何时能进入港口?在港口能停留多久?


 (2012•宿州三模)某校一研究性学习小组对宿州市工薪阶层关于“楼市限购令”态度进行调查,随机抽调了50人,他们月收入频数分布及对“楼市限购令”赞成人数如表:
(2012•宿州三模)某校一研究性学习小组对宿州市工薪阶层关于“楼市限购令”态度进行调查,随机抽调了50人,他们月收入频数分布及对“楼市限购令”赞成人数如表: