题目内容
1.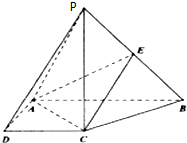 如图,在四棱锥P-ABCD.中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2.E是PB的中点.
如图,在四棱锥P-ABCD.中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2.E是PB的中点.(Ⅰ)求证;平面EAC⊥平面PBC;
(Ⅱ)若二面角P-AC-E的余弦值为$\frac{\sqrt{3}}{3}$,求直线PA与平面EAC所成角的正弦值.
分析 (I)通过证明AC⊥平面PBC,利用平面与平面垂直的判定定理证明平面EAC⊥平面PBC.
( II)如图,以C为原点,$\overrightarrow{DA}$、$\overrightarrow{CD}$、$\overrightarrow{CP}$分别为x轴、y轴、z轴正向,建立空间直角坐标系,求出相关点的坐标,设P(0,0,a)(a>0),求出面PAC的法向量$\overrightarrow{m}$=(1,-1,0),设$\overrightarrow{n}$=(x,y,z)为面EAC的法向量,利用$\overrightarrow{n}$•$\overrightarrow{CA}$=$\overrightarrow{n}$•$\overrightarrow{CE}$=0,求出$\overrightarrow{n}$=(a,-a,-2),利用向量的数量积求解,即可得到直线PA与平面EAC所成角的正弦值.
解答 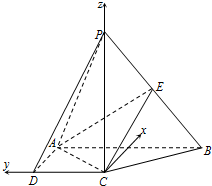 解:(I)证明:∵PC⊥平面ABCD,AC?平面ABCD,∴AC⊥PC,
解:(I)证明:∵PC⊥平面ABCD,AC?平面ABCD,∴AC⊥PC,
∵AB=2,AD=CD=2,∴AC=BC=$\sqrt{2}$,
∴AC2+BC2=AB2,∴AC⊥BC,
又BC∩PC=C,∴AC⊥平面PBC,
∵AC?平面EAC,∴平面EAC⊥平面PBC.-----------(4分)
( II)解:如图,以C为原点,$\overrightarrow{DA}$、$\overrightarrow{CD}$、$\overrightarrow{CP}$分别为x轴、y轴、z轴正向,建立空间直角坐标系,则C(0,0,0),A(1,1,0),B(1,-1,0).
设P(0,0,a)(a>0),则E($\frac{1}{2}$,-$\frac{1}{2}$,$\frac{a}{2}$),-----------(6分)
$\overrightarrow{CA}$=(1,1,0),$\overrightarrow{CP}$=(0,0,a),
$\overrightarrow{CE}$=($\frac{1}{2}$,-$\frac{1}{2}$,$\frac{a}{2}$),
取$\overrightarrow{m}$=(1,-1,0),则
$\overrightarrow{m}$•$\overrightarrow{CA}$=$\overrightarrow{m}$•$\overrightarrow{CP}$=0,$\overrightarrow{m}$为面PAC的法向量.
设$\overrightarrow{n}$=(x,y,z)为面EAC的法向量,则$\overrightarrow{n}$•$\overrightarrow{CA}$=$\overrightarrow{n}$•$\overrightarrow{CE}$=0,
即$\left\{\begin{array}{l}x+y=0\\ x-y+az=0\end{array}$取x=a,y=-a,z=-2,则$\overrightarrow{n}$=(a,-a,-2),
依题意,|cos<$\overrightarrow{m}$,$\overrightarrow{n}$>|=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{a}{\sqrt{{a}^{2}+2}}$=$\frac{{\sqrt{3}}}{3}$,则a=1.-----------(10分)
于是$\overrightarrow{n}$=(1,-1,-2),$\overrightarrow{PA}$=(1,1,-1).
设直线PA与平面EAC所成角为θ,
则sinθ=|cos<$\overrightarrow{PA}$,$\overrightarrow{n}$>|=$\frac{\overrightarrow{PA}•\overrightarrow{n}}{\left|\overrightarrow{PA}\right|\left|\overrightarrow{n}\right|}$=$\frac{2}{\sqrt{3}•\sqrt{6}}$=$\frac{\sqrt{2}}{3}$,
即直线PA与平面EAC所成角的正弦值为$\frac{\sqrt{2}}{3}$.-----------(12分)
点评 本题考查二面角以及直线与平面所成角的求法与应用,平面与平面垂直的判定定理以及直线与平面垂直的判定定理的应用,考查空间想象能力以及计算能力.

| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 非奇非偶函数 |
| A. | $\frac{16}{17}$ | B. | $\frac{36}{5}$ | C. | $\frac{26}{5}$ | D. | $\frac{196}{53}$ |
| A. | 1 | B. | $\frac{1}{16}$ | C. | $\frac{1}{2}$ | D. | 1或$\frac{1}{16}$ |
| A. | “至少有一本是数学书”与“都是数学书” | |
| B. | “至少有一本是数学书”与“都是语文书” | |
| C. | “至少有一本是数学书”与“至少有1本是语文书” | |
| D. | “恰有1本是数学书”与“恰有2本是语文书” |