题目内容
设函数f(x)=sin2x+cos2x+1.
(1)求函数f(x)的周期和最大值;
(2)设ABCD的内角A、B、C的对应边分别为a、b、c,若a=1,b=2
,f(C)=2,求边长c及sinA的值.
(1)求函数f(x)的周期和最大值;
(2)设ABCD的内角A、B、C的对应边分别为a、b、c,若a=1,b=2
| 2 |
分析:(1)利用辅助角公式,化简函数,即可求函数f(x)的周期和最大值;
(2)先求C,再利用余弦定理,求出c,利用正弦定理,可求sinA的值.
(2)先求C,再利用余弦定理,求出c,利用正弦定理,可求sinA的值.
解答:解:(1)f(x)=sin2x+cos2x+1=
(
cos2x+
sin2x)+1=
sin(2x+
)+1. …(2分)
∴f(x)的周期T=π,f(x)max=
+1…(4分)
(2)由f(C)=
sin(2C+
)+1=2,得sin(2C+
)=
…(5分)
∵0<C<π,∴
<2C+
<2π+
,∴2C+
=
.…(6分)
∴C=
. …(7分)
由余弦定理得:c2=a2+b2-2abcosC=12+(2
)2-2×1×2
cos
=5…(9分)
∴c=
…(10分)
由正弦定理得:
=
,…(11分)
即
=
,所以sinA=
.…(12分)
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| π |
| 4 |
∴f(x)的周期T=π,f(x)max=
| 2 |
(2)由f(C)=
| 2 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
∵0<C<π,∴
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴C=
| π |
| 4 |
由余弦定理得:c2=a2+b2-2abcosC=12+(2
| 2 |
| 2 |
| π |
| 4 |
∴c=
| 5 |
由正弦定理得:
| a |
| sinA |
| c |
| sinC |
即
| 1 |
| sinA |
| ||||
|
| ||
| 10 |
点评:本题考查三角函数的化简,考查三角函数的性质,考查余弦定理、正弦定理的运用,属于中档题.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 )-cos2(x+
)-cos2(x+ )(x∈R),则函数f(x)是( )
)(x∈R),则函数f(x)是( ) 的奇函数
的奇函数 的偶函数
的偶函数 sinωx•cosωx-cos2ωx+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(
sinωx•cosωx-cos2ωx+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈( ,1).
,1). ,求函数f(x)的值域.
,求函数f(x)的值域.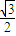 -
- sin2ωx-sinωxcosωx(ω>0),且y=f(x)的图象的一个对称中心到最近的对称轴的距离为
sin2ωx-sinωxcosωx(ω>0),且y=f(x)的图象的一个对称中心到最近的对称轴的距离为 ,
, ]上的最大值和最小值.
]上的最大值和最小值.