题目内容
已知函数 在点(x1,f(x1))处的切线在x轴上的截距为x2,则当
在点(x1,f(x1))处的切线在x轴上的截距为x2,则当 时,
时, 的取值范围是 .
的取值范围是 .
【答案】分析:已知函数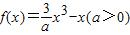 ,对f(x)进行求导,求出f(x)在x=x1处的导数,根据点斜式求出切线方程,求出截距x2,再利用不等式进行求解;
,对f(x)进行求导,求出f(x)在x=x1处的导数,根据点斜式求出切线方程,求出截距x2,再利用不等式进行求解;
解答:解:∵已知函数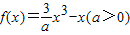 ,
,
∴f′(x)=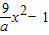 ,a>0,
,a>0,
∵在点(x1,f(x1))处的切线,
∴切线斜率为:k=f′(x)|x=x1=f′(x1)=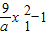 ,
,
切线方程:y-f(x1)=f′(x1)(x-x1),
∴令y=0,得x2=x1-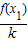 =x1-
=x1-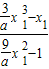 =
=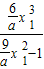 ,
,
∴y=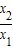 =
=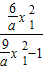 =
=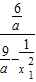 ,当
,当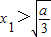 时,y为减函数,
时,y为减函数,
∴y<f(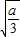 )=1,
)=1,
又∵y=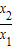 =
=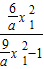 =
=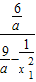 >
>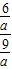 =
= ,
,
∴ <
<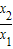 <1,
<1,
故答案为: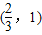 ;
;
点评:此题主要考查利用导数研究函数的切线方程,主要利用了不等式的放缩,还间接考查函数的单调性问题,此题是一道好题;
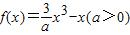 ,对f(x)进行求导,求出f(x)在x=x1处的导数,根据点斜式求出切线方程,求出截距x2,再利用不等式进行求解;
,对f(x)进行求导,求出f(x)在x=x1处的导数,根据点斜式求出切线方程,求出截距x2,再利用不等式进行求解;解答:解:∵已知函数
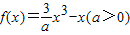 ,
,∴f′(x)=
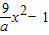 ,a>0,
,a>0,∵在点(x1,f(x1))处的切线,
∴切线斜率为:k=f′(x)|x=x1=f′(x1)=
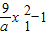 ,
,切线方程:y-f(x1)=f′(x1)(x-x1),
∴令y=0,得x2=x1-
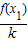 =x1-
=x1-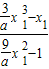 =
=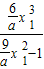 ,
,∴y=
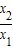 =
=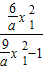 =
=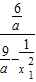 ,当
,当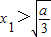 时,y为减函数,
时,y为减函数,∴y<f(
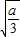 )=1,
)=1,又∵y=
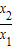 =
=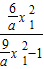 =
=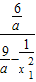 >
>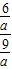 =
= ,
,∴
 <
<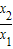 <1,
<1,故答案为:
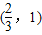 ;
;点评:此题主要考查利用导数研究函数的切线方程,主要利用了不等式的放缩,还间接考查函数的单调性问题,此题是一道好题;

练习册系列答案
相关题目
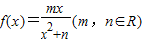 在x=1处取得极值2,
在x=1处取得极值2,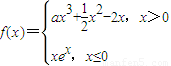 在点A(1,f(1))处的切线l的斜率为零.
在点A(1,f(1))处的切线l的斜率为零.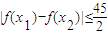 恒成立,这样的m是否存在?若存在,请求出m的取值范围;若不存在,请说明理由.
恒成立,这样的m是否存在?若存在,请求出m的取值范围;若不存在,请说明理由. 在x=1处取得极值2,
在x=1处取得极值2, 在点(x1,f(x1))处的切线在x轴上的截距为x2,则当
在点(x1,f(x1))处的切线在x轴上的截距为x2,则当 时,
时, 的取值范围是_________.
的取值范围是_________.