Question

已知函数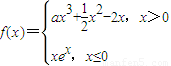在点A（1，f（1））处的切线l的斜率为零．
（Ⅰ）求a的值；
（Ⅱ）求f（x）的单调区间；
（Ⅲ）若对任意的x₁，x₂∈[m，m+3]，不等式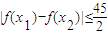恒成立，这样的m是否存在？若存在，请求出m的取值范围；若不存在，请说明理由．

Answer 1

【答案】分析：（Ⅰ）求出x＞0时的f'（x），再由f'（1）=0求出a的值；
（Ⅱ）把a的值代入解析式，分别求x＞0时和x≤0时函数的导数f'（x），再求出f'（x）＞0和f'（x）＜0对应的x范围，求出函数的单调区间；
（Ⅲ）根据（Ⅱ）求出的单调区间，对m进行分三类进行讨论：当m＞1时、当0＜m≤1时，当m≤0时，利用在区间[m，m+3]上的单调性，分别求出最大值和最小值，然后作差判断是否满足，最后再三种结果并在一起．
解答：解：（Ⅰ）由题意当x＞0时，f'（x）=3ax²+x-2，且f'（1）=0，
∴3a+1-2=0，解得，
（Ⅱ）由（Ⅰ）知，                                             
当x＞0时，f'（x）=x²+x-2=（x+2）（x-1），
∴x∈[0，1）时，f'（x）＜0；x∈（1，+∞）时f'（x）＞0．                            
当x≤0时，f'（x）=xe^x+e^x=（x+1）e^x，
∴x∈（-∞，-1）时f'（x）＜0；x∈（-1，0）时f'（x）＞0．                           
∴f（x）在（-1，0），（1，+∞）上单调递增；
在[0，1），（-∞，-1）上单调递减．                                                
（Ⅲ）由（Ⅱ）知，①当m＞1时，f（x）在[m，m+3]上递增，
故f_max（x）=f（m+3），f_min（x）=f（m），
由
=
=，
∵m＞1，∴3（m+2）²，
即，此时m不存在，
②当0＜m≤1时，f（x）在[m，1]上递减，在[1，m+3]上递增，
故．
∴，
∴0＜m≤1时，符合题意．                                                          
③当m≤0时，m+3≤3，
∴．0≤x＜3时，；
x＜0时，f（-1）≤f（x）＜0，即．
∴x₁，x₂∈[m，m+3]时，，
∴m≤0时，符合题意．                                                            
综上，存在m∈（-∞，1]使原不等式恒成立．
点评：本题考查了导数的几何意义，导数与函数的单调性关系，以及恒成立问题转化为求最值等综合应用，考查了分类讨论思想和转化思想，难度较大．