题目内容
【题目】设![]() ,函数
,函数![]() .
.
(1)若![]() 无零点,求实数
无零点,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 有两个相异零点
有两个相异零点![]() ,
,![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)通过a的值,利用函数的导数的符号,结合函数的单调性,判断函数的零点,求解即可.(2)利用x1,x2是方程alnx﹣x=0的两个不同的实数根.得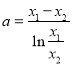 要证:
要证:![]() ,即证:
,即证:![]() ,即证:
,即证: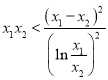 ,构造函数
,构造函数
,求出导函数;求其最值,推出转化证明求解即可.
(1)①若![]() ,则
,则![]() ,
,![]() 是区间
是区间![]() 上的减函数,
上的减函数,
∵![]() ,
, ,
,
而![]() ,则
,则![]() ,即
,即
∴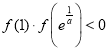 ,函数
,函数![]() 在区间
在区间![]() 有唯一零点;
有唯一零点;
②若![]() ,
,![]() ,在区间
,在区间![]() 无零点;
无零点;
③若![]() ,令
,令![]() ,得
,得![]() ,
,
在区间![]() 上,
上,![]() ,函数
,函数![]() 是增函数;
是增函数;
在区间![]() 上,
上,![]() ,函数
,函数![]() 是减函数;
是减函数;
故在区间![]() 上,
上,![]() 的最大值为
的最大值为![]() ,由于
,由于![]() 无零点,
无零点,
则![]() ,解得
,解得![]() ,
,
故所求实数![]() 的取值范围是
的取值范围是![]() .
.
(2)因为![]() ,
,![]() 是方程
是方程![]() 的两个不同的实数根.
的两个不同的实数根.
∴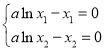
两式相减得![]() ,解得
,解得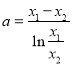
要证:![]() ,即证:
,即证:![]() ,即证:
,即证: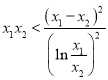 ,
,
即证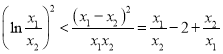 ,
,
不妨设![]() ,令
,令![]() ,只需证
,只需证![]() .
.
设![]() ,∴
,∴![]() ;
;
令![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 上单调递减,∴
上单调递减,∴![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 为增函数,∴
为增函数,∴![]()
即![]() 在
在![]() 恒成立,
恒成立,
∴原不等式成立,即![]() .
.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案【题目】某种计算机病毒是通过电子邮件进行传播的,下表是某公司前5天监测到的数据:
第 | 1 | 2 | 3 | 4 | 5 |
被感染的计算机数量 | 10 | 20 | 39 | 81 | 160 |
则下列函数模型中,能较好地反映计算机在第![]() 天被感染的数量
天被感染的数量![]() 与
与![]() 之间的关系的是
之间的关系的是
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【题目】近年来,随着互联网的发展,诸如“滴滴打车”“神州专车”等网约车服务在我国各城市迅猛发展,为人们出行提供了便利,但也给城市交通管理带来了一些困难.为掌握网约车在![]() 省的发展情况,
省的发展情况,![]() 省某调查机构从该省抽取了5个城市,分别收集和分析了网约车的
省某调查机构从该省抽取了5个城市,分别收集和分析了网约车的![]() ,
,![]() 两项指标数
两项指标数![]() ,数据如下表所示:
,数据如下表所示:
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
| 2 | 4 | 5 | 6 | 8 |
| 3 | 4 | 4 | 4 | 5 |
经计算得: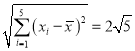 ,
,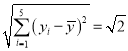 ,
,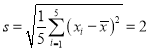 .
.
(1)试求![]() 与
与![]() 间的相关系数
间的相关系数![]() ,并利用
,并利用![]() 说明
说明![]() 与
与![]() 是否具有较强的线性相关关系(若
是否具有较强的线性相关关系(若![]() ,则线性相关程度很高,可用线性回归模型拟合);
,则线性相关程度很高,可用线性回归模型拟合);
(2)建立![]() 关于
关于![]() 的回归方程,并预测当
的回归方程,并预测当![]() 指标数为7时,
指标数为7时,![]() 指标数的估计值;
指标数的估计值;
(3)若城市的网约车![]() 指标数
指标数![]() 落在区间
落在区间![]() 之外,则认为该城市网约车数量过多,会对城市交通管理带来较大的影响,交通管理部门将介入进行治理,直至
之外,则认为该城市网约车数量过多,会对城市交通管理带来较大的影响,交通管理部门将介入进行治理,直至![]() 指标数
指标数![]() 回落到区间
回落到区间![]() 之内.现已知2018年11月该城市网约车的
之内.现已知2018年11月该城市网约车的![]() 指标数为13,问:该城市的交通管理部门是否要介入进行治理?试说明理由.
指标数为13,问:该城市的交通管理部门是否要介入进行治理?试说明理由.
附:相关公式: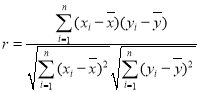 ,
,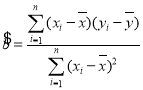 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.


