题目内容
△ABC中，点M是边BC的中点，|
|=
，|
|=1，则
•
= ．
| AB |
| 3 |
| AC |
| AM |
| BC |
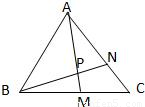
分析：如图所示，在△ABC中，由于点M是边BC的中点，利用向量的平行四边形法则和三角形法则
=
(
+
)、
=
-
．再利用数量积运算即可得出．
| AM |
| 1 |
| 2 |
| AB |
| AC |
| BC |
| AC |
| AB |
解答：解：如图所示，
在△ABC中，∵点M是边BC的中点，
∴
=
(
+
)．
又
=
-
．
∴
•
=
(
+
)•(
-
)=
(
2-
2)=
[12-(
)2]=-1．
故答案为：-1．
在△ABC中，∵点M是边BC的中点，
∴
| AM |
| 1 |
| 2 |
| AB |
| AC |
又
| BC |
| AC |
| AB |
∴
| AM |
| BC |
| 1 |
| 2 |
| AC |
| AB |
| AC |
| AB |
| 1 |
| 2 |
| AC |
| AB |
| 1 |
| 2 |
| 3 |
故答案为：-1．
点评：本题考查了向量的平行四边形法则和三角形法则、数量积运算性质，属于基础题．
练习册系列答案
教材全解字词句篇系列答案
相关题目
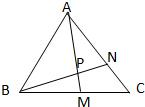如图，在△ABC中，点M是BC的中点，点N在边AC上，且AN=2NC，AM与BN相交于点P，则点P分有向线段
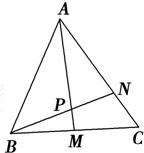如图所示，在△ABC中，点M是BC的中点，点N在边AC上，且AN=2NC，AM与BN相交于点P，求AP：PM的值．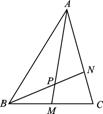
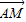所成的比为 ．