题目内容
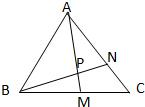如图，在△ABC中，点M是BC的中点，点N在边AC上，且AN=2NC，AM与BN相交于点P，则点P分有向线段| AM |
分析：设
=
，
=
，求出
和
的解析式，由三点共线得
=λ
，
=μ
，进而求出
的解析式，又
=
+
=2
+3
，比较系数，建立关于λ、μ的方程，解方程求λ、μ的值，结果可得．
| BM |
| a |
| CN |
| b |
| AM |
| BN |
| AP |
| AM |
| BP |
| BN |
| BA |
| BA |
| BC |
| CA |
| a |
| b |
解答：解：如图：设
=
，
=
，点M是BC的中点，点N在边AC上，且AN=2NC，
则
=
+
=-3
-
，
=
+
=2
+
，
∵A、P、M共线，B、N、P 共线，∴存在λ、μ使
=λ
=-λ
-3λ
，
=μ
=2μ
+μ
，
∴
=
-
=（2μ+λ）
+（μ+3λ）
，
又
=
+
=2
+3
，∴
，
∴
，∴
=
，∴
：
=4，
故答案为：4．
解：如图：设| BM |
| a |
| CN |
| b |
则
| AM |
| AC |
| CM |
| b |
| a |
| BN |
| BC |
| CN |
| a |
| b |
∵A、P、M共线，B、N、P 共线，∴存在λ、μ使
| AP |
| AM |
| a |
| b |
| BP |
| BN |
| a |
| b |
∴
| BA |
| BP |
| AP |
| a |
| b |
又
| BA |
| BC |
| CA |
| a |
| b |
|
∴
|
| AP |
| 4 |
| 5 |
| AM |
| AP |
| PM |
故答案为：4．
点评：本题考查平面向量基本定理的应用，三点共线的性质以及定比分点的定义．
练习册系列答案
相关题目
如图，在△ABC中，已知∠ABC=90°，AB上一点E，以BE为直径的⊙O恰与AC相切于点D，若AE=2cm，
如图，在△ABC中，D是边AC上的点，且AB=AD，2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，在△ABC中，设
如图，在△ABC中，∠B=45°，D是BC边上的一点，AD=5，AC=7，DC=3．
如图，在△ABC中，已知