题目内容
如果不等式（m+1）x2+2mx+m+1＞0对任意实数x都成立，则实数m的取值范围是（ ）A．m＞-1
B．
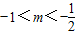
C．
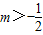
D．m＜-1或
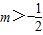
【答案】分析：当m+1=0时，经检验不满足条件．当m≠0时，由题意可得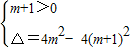
，由此求得实数m的取值范围．
解答：解：当m+1=0时，不等式即-2x＞0，显然不满足对任意实数x都成立．
当m≠0时，由不等式（m+1）x2+2mx+m+1＞0对任意实数x都成立，可得m+1＞0，且判别式△＜0．
即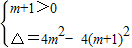
，解得 m＞-
，
故选C．
点评：本题主要考查一元二次不等式，函数的恒成立问题，体现了分类讨论的数学思想，属于基础题．
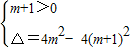，由此求得实数m的取值范围．解答：解：当m+1=0时，不等式即-2x＞0，显然不满足对任意实数x都成立．
当m≠0时，由不等式（m+1）x2+2mx+m+1＞0对任意实数x都成立，可得m+1＞0，且判别式△＜0．
即
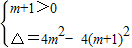，解得 m＞-，故选C．
点评：本题主要考查一元二次不等式，函数的恒成立问题，体现了分类讨论的数学思想，属于基础题．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
相关题目
