题目内容
如果两个椭圆的离心率相等,那么就称这两个椭圆相似.已知椭圆C与椭圆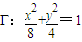 相似,且椭圆C的一个短轴端点是抛物线
相似,且椭圆C的一个短轴端点是抛物线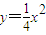 的焦点.
的焦点.(Ⅰ)试求椭圆C的标准方程;
(Ⅱ)设椭圆E的中心在原点,对称轴在坐标轴上,直线l:y=kx+t(k≠0,t≠0)与椭圆C交于A,B两点,且与椭圆E交于H,K两点.若线段AB与线段HK的中点重合,试判断椭圆C与椭圆E是否为相似椭圆?并证明你的判断.
【答案】分析:(Ⅰ)求出椭圆的离心率,抛物线的焦点坐标,设椭圆C的方程,即可求得椭圆的几何量,从而可求椭圆C的标准方;
(Ⅱ)解法一:椭圆C与椭圆E是相似椭圆.联立椭圆C和直线l的方程,利用韦达定理,根据弦AB的中点与弦HK的中点重合,建立方程,从而可得椭圆E的离心率,即可得到结论;
解法二:设椭圆E的方程,根据A,B在椭圆C上,设点的坐标,代入两式相减并恒等变形得斜率,同理由H,K在椭圆E上,得斜率,利用弦AB的中点与弦HK的中点重合,建立方程,从而可得椭圆E的离心率,即可得到结论.
解答:解:(Ⅰ)由题意,椭圆 的离心率为
的离心率为 ,抛物线
,抛物线 的焦点为(0,1).…(2分)
的焦点为(0,1).…(2分)
设椭圆C的方程为 ,
,
由题意,得: ,解得
,解得 ,
,
∴椭圆C的标准方程为 .…(5分)
.…(5分)
(Ⅱ)解法一:椭圆C与椭圆E是相似椭圆.…(6分)
联立椭圆C和直线l的方程, ,消去y,得(1+2k2)x2+4ktx+2t2-8=0,…(7分)
,消去y,得(1+2k2)x2+4ktx+2t2-8=0,…(7分)
设A,B的横坐标分别为x1,x2,则 .…(8分)
.…(8分)
设椭圆E的方程为 ,…(9分)
,…(9分)
联立方程组 ,消去y,得(n2+m2k2)x2+2ktm2x+m2(t2-n2)=0,
,消去y,得(n2+m2k2)x2+2ktm2x+m2(t2-n2)=0,
设H,K的横坐标分别为x3,x4,则 .…(10分)
.…(10分)
∵弦AB的中点与弦HK的中点重合,…(11分)
∴x1+x2=x3+x4,∴ =
= ,
,
∵k≠0,t≠0,∴化简得m2=2n2,…(12分)
求得椭圆E的离心率 ,…(13分)
,…(13分)
∴椭圆C与椭圆E是相似椭圆.
解法二:设椭圆E的方程为 ,并设A(x1,y1),B(x2,y2),H(x3,y3),K(x4,y4).
,并设A(x1,y1),B(x2,y2),H(x3,y3),K(x4,y4).
∵A,B在椭圆C上,
∴ 且
且 ,两式相减并恒等变形得
,两式相减并恒等变形得 .…(8分)
.…(8分)
由H,K在椭圆E上,仿前述方法可得 .…(11分)
.…(11分)
∵弦AB的中点与弦HK的中点重合,∴m2=2n2,…(12分)
求得椭圆E的离心率 ,…(13分)
,…(13分)
∴椭圆C与椭圆E是相似椭圆.
点评:本题主要考查椭圆的标准方程、圆锥曲线的性质、直线与圆锥曲线的位置关系等基础知识,考查推理论证能力、运算求解能力,考查分类整合思想、数形结合思想、化归转化思想等.
(Ⅱ)解法一:椭圆C与椭圆E是相似椭圆.联立椭圆C和直线l的方程,利用韦达定理,根据弦AB的中点与弦HK的中点重合,建立方程,从而可得椭圆E的离心率,即可得到结论;
解法二:设椭圆E的方程,根据A,B在椭圆C上,设点的坐标,代入两式相减并恒等变形得斜率,同理由H,K在椭圆E上,得斜率,利用弦AB的中点与弦HK的中点重合,建立方程,从而可得椭圆E的离心率,即可得到结论.
解答:解:(Ⅰ)由题意,椭圆
 的离心率为
的离心率为 ,抛物线
,抛物线 的焦点为(0,1).…(2分)
的焦点为(0,1).…(2分)设椭圆C的方程为
 ,
,由题意,得:
 ,解得
,解得 ,
,∴椭圆C的标准方程为
 .…(5分)
.…(5分)(Ⅱ)解法一:椭圆C与椭圆E是相似椭圆.…(6分)
联立椭圆C和直线l的方程,
 ,消去y,得(1+2k2)x2+4ktx+2t2-8=0,…(7分)
,消去y,得(1+2k2)x2+4ktx+2t2-8=0,…(7分)设A,B的横坐标分别为x1,x2,则
 .…(8分)
.…(8分)设椭圆E的方程为
 ,…(9分)
,…(9分)联立方程组
 ,消去y,得(n2+m2k2)x2+2ktm2x+m2(t2-n2)=0,
,消去y,得(n2+m2k2)x2+2ktm2x+m2(t2-n2)=0,设H,K的横坐标分别为x3,x4,则
 .…(10分)
.…(10分)∵弦AB的中点与弦HK的中点重合,…(11分)
∴x1+x2=x3+x4,∴
 =
= ,
,∵k≠0,t≠0,∴化简得m2=2n2,…(12分)
求得椭圆E的离心率
 ,…(13分)
,…(13分)∴椭圆C与椭圆E是相似椭圆.
解法二:设椭圆E的方程为
 ,并设A(x1,y1),B(x2,y2),H(x3,y3),K(x4,y4).
,并设A(x1,y1),B(x2,y2),H(x3,y3),K(x4,y4).∵A,B在椭圆C上,
∴
 且
且 ,两式相减并恒等变形得
,两式相减并恒等变形得 .…(8分)
.…(8分)由H,K在椭圆E上,仿前述方法可得
 .…(11分)
.…(11分)∵弦AB的中点与弦HK的中点重合,∴m2=2n2,…(12分)
求得椭圆E的离心率
 ,…(13分)
,…(13分)∴椭圆C与椭圆E是相似椭圆.
点评:本题主要考查椭圆的标准方程、圆锥曲线的性质、直线与圆锥曲线的位置关系等基础知识,考查推理论证能力、运算求解能力,考查分类整合思想、数形结合思想、化归转化思想等.

练习册系列答案
相关题目
 与椭圆
与椭圆 相似,且椭圆
相似,且椭圆 的焦点.
的焦点. 的中心在原点,对称轴在坐标轴上,直线
的中心在原点,对称轴在坐标轴上,直线 与椭圆
与椭圆 两点,且与椭圆
两点,且与椭圆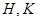 两点.若线段
两点.若线段 与线段
与线段 的中点重合,试判断椭圆
的中点重合,试判断椭圆