题目内容
已知a>0,函数f(x)=ax-bx2.(1)当b>0时,若对任意x∈R都有f(x)≤1,证明![]() ;
;
(2)当b>1时,证明对任意x∈[0,1],|f(x)|≤1的充要条件是b-1≤a≤![]() ;
;
(3)当0<b≤1时,讨论:对任意x∈[0,1],|f(x)|≤1的充要条件.
(1)证明:依题意知,对任意x∈R,都有f(x)≤1.
∵![]() ,∴
,∴![]() .
.
∵a>0,b>0,∴![]() .
.
(2)证明:必要性:对任意x∈[0,1],|f(x)|≤1![]() f(x)≥-1,
f(x)≥-1,
∴f(1)≥-1,即a-b≥-1.∴a≥b-1.
对任意x∈[0,1],|f(x)|≤1![]() f(x)≤1,
f(x)≤1,
∵b>1,可以推出![]() ,
,
即![]() ,∴
,∴![]() .∴b-1≤a≤
.∴b-1≤a≤![]() .
.
充分性:∵b>1,a≥b-1,对任意x∈[0,1],可以推出ax-bx2≥b(x-x2)-x≥-x≥-1,即ax-?bx2≥-1.
∵b>1, ![]() .对任意x∈[0,1],可以推出ax-bx2≤
.对任意x∈[0,1],可以推出ax-bx2≤![]() x-bx2≤1,
x-bx2≤1,
即ax-bx2≤1.∴-1≤f(x)≤1.
综上,当b>1时,对任意x∈[0,1],|f(x)|≤1的充要条件是b-1≤a≤![]() .
.
(3)解:∵a>0,0<b≤1时,对任意x∈[0,1],有f(x)=ax-bx2≥-b≥-1,
即f(x)≥-1.
f(x)≤1![]() f(1)≤1
f(1)≤1![]() a-b≤1,即a≤1+b.
a-b≤1,即a≤1+b.
a≤1+b![]() f(x)≤(1+b)x-bx2≤1,即f(x)≤1.
f(x)≤(1+b)x-bx2≤1,即f(x)≤1.
∴当a>0,0<b≤1时,对任意x∈[0,1],|f(x)|≤1的充要条件是a≤1+b.
启示:本题主要考查二次函数、不等式、充要条件的综合应用,考查分类讨论思想和逻辑推理能力以及思维能力.

练习册系列答案
相关题目
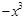 +ax在[1,+∞)上是减函数,则a的取值范围是(
)
+ax在[1,+∞)上是减函数,则a的取值范围是(
)