题目内容
(16分)已知函数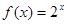
(1)试求函数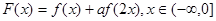 的最大值;
的最大值;
(2)若存在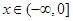 ,使
,使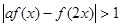 成立,试求
成立,试求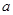 的取值范围;
的取值范围;
(3)当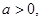 且
且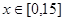 时,不等式
时,不等式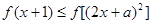 恒成立,求
恒成立,求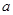 的取值范围;
的取值范围;
【答案】
(1)
(2)
(3)
【解析】(1)根据f(x)的表达式求得F(x)的表达式,然后根据分段函数的知识求出函数F(x)d的最大值;(2)先根据绝对值不等式知识去掉绝对值,然后由不等式有解求出a的取值范围;(3)先根据恒成立转化为求最值问题,在利用换元法求出一元二次函数的最值,即参数a的取值范围
解:(1)
(2)令 则存在
则存在 使得
使得 ,所以存在
,所以存在 使得
使得 即存在
即存在 使得
使得

(3)由 得
得 恒成立
恒成立
因为 且
且 ,所以问题即为
,所以问题即为 恒成立
恒成立


设
 ,令
,令

所以当t=1时, ,
,

练习册系列答案
相关题目

 的值.
的值.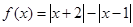
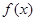 的值域;
的值域;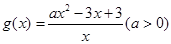 ,若对
,若对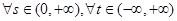 恒有
恒有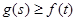 成立,试求实数
成立,试求实数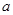 的取值氛围。
的取值氛围。
 有唯一解,求a的取值范围.
有唯一解,求a的取值范围.