题目内容
已知椭圆的中心在原点,对称轴为坐标轴,其左焦点为F,长轴长为4,左顶点到左准线的距离与左顶点到左焦点的距离之比为2∶(1)求椭圆的方程;
(2)求|![]() |的取值范围.
|的取值范围.
解:(1)设椭圆方程为![]() =1(a>b>0),
=1(a>b>0),
则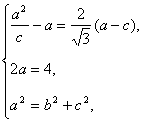
解得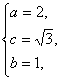 ∴椭圆方程为
∴椭圆方程为![]() +y2=1.
+y2=1.
(2)设直线l为x=my![]() ,代入
,代入![]() +y2=1整理,得
+y2=1整理,得
(m2+4)y2-2![]() my-1=0.
my-1=0.
设P(x1,y1),Q(x2,y2),则|y1-y2|=![]() =
=![]() .
.
x1x2=(my1-![]() )(my2-
)(my2-![]() )=m2y1y2-
)=m2y1y2-![]() m(y1+y2)+3=
m(y1+y2)+3=![]() .
.
又ym=![]() ·
·![]() ,yn=
,yn=![]() ·
·![]() ,∴|MN|=|ym-yn|=
,∴|MN|=|ym-yn|=![]() |
|![]() |
|
=![]() |
|![]() |=4|
|=4|![]() |=
|=![]() .
.
令t=![]() ,∴|MN|=
,∴|MN|=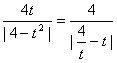 (t≥1).∵
(t≥1).∵![]() ≤α≤
≤α≤![]() ,m=cotα,
,m=cotα,
∴当α=![]() 时,l与准线不相交,故m≠0.∴0<m2≤
时,l与准线不相交,故m≠0.∴0<m2≤![]() .∴1<t≤
.∴1<t≤![]() .
.
∵u=![]() -t在(1,
-t在(1,![]() ]上递减,∴
]上递减,∴![]() <u≤3,则
<u≤3,则![]() <|
<|![]() |≤
|≤![]() .
.

练习册系列答案
相关题目