题目内容
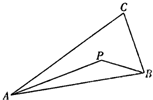
如图，设P为△ABC内一点，且
=
+
，则
=（ ）
| AP |
| 2 |
| 5 |
| AB |
| 1 |
| 5 |
| AC |
| S△ABP |
| S△ABC |
A．
| B．
| C．
| D．
|
连接CP并延长，交AB于D，过P作PM∥AB交AC于M，过P作PN∥AC交AB于N，
因为设P为△ABC内一点，且
=
+
，
可得AM=
AC，
在三角形ACD中由PM∥AD可得即
=4
，
故
=5
，
则△ABP的面积与△ABC面积之比为
．
故选A．
因为设P为△ABC内一点，且
| AP |
| 2 |
| 5 |
| AB |
| 1 |
| 5 |
| AC |
可得AM=
| 1 |
| 5 |
在三角形ACD中由PM∥AD可得即
| CP |
| PD |
故
| CD |
| PD |
则△ABP的面积与△ABC面积之比为
| 1 |
| 5 |
故选A．
练习册系列答案
相关题目
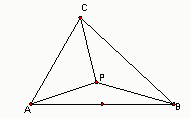
如图，设P为△ABC内一点，且2
+2
+
=
，则△ABP的面积与△ABC的面积之比为（ ）
| PA |
| PB |
| PC |
| 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，设P为△ABC内一点，且
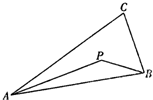
，则△ABP的面积与△ABC的面积之比为（ ）
