题目内容
已知函数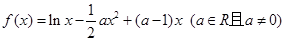
(1)当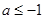 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;
(2)记函数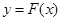 的图象为曲线
的图象为曲线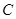 ,设点
,设点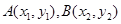 是曲线
是曲线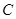 上的不同两点.如果在曲线
上的不同两点.如果在曲线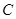 上存在点
上存在点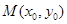 ,使得:①
,使得:①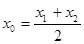 ;②曲线
;②曲线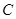 在点
在点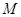 处的切线平行于直线
处的切线平行于直线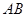 ,则称函数
,则称函数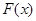 存在“中值相依切线”,试问:函数
存在“中值相依切线”,试问:函数 是否存在“中值相依切线”,请说明理由.
是否存在“中值相依切线”,请说明理由.
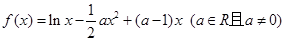
(1)当
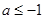 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;(2)记函数
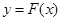 的图象为曲线
的图象为曲线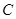 ,设点
,设点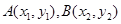 是曲线
是曲线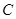 上的不同两点.如果在曲线
上的不同两点.如果在曲线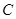 上存在点
上存在点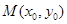 ,使得:①
,使得:①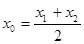 ;②曲线
;②曲线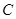 在点
在点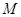 处的切线平行于直线
处的切线平行于直线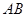 ,则称函数
,则称函数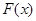 存在“中值相依切线”,试问:函数
存在“中值相依切线”,试问:函数 是否存在“中值相依切线”,请说明理由.
是否存在“中值相依切线”,请说明理由.(1)当 时,
时, 的单调递增区间为
的单调递增区间为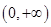 ;当
;当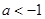 ,
, 的单调递增区间为
的单调递增区间为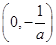 和
和 ;(2)函数
;(2)函数 不存在“中值相依切线”.
不存在“中值相依切线”.
 时,
时, 的单调递增区间为
的单调递增区间为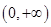 ;当
;当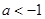 ,
, 的单调递增区间为
的单调递增区间为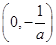 和
和 ;(2)函数
;(2)函数 不存在“中值相依切线”.
不存在“中值相依切线”.试题分析:(1)当
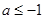 时,分
时,分 和
和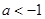 两种情况分别进行分析,当
两种情况分别进行分析,当 时,
时, 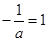 , 显然函数
, 显然函数 在
在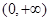 上单调递增;当
上单调递增;当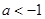 时,
时, 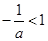 ,令
,令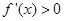 ,解得
,解得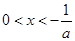 或
或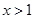 ;所以当
;所以当 时,函数
时,函数 在
在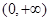 上单调递增;当
上单调递增;当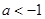 时,函数
时,函数 在
在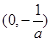 和
和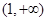 上单调递增;(2)先设
上单调递增;(2)先设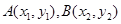 是曲线
是曲线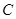 上的不同两点,求出
上的不同两点,求出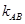 的表达式化简得到:
的表达式化简得到: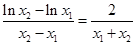 ,再经过求导分析得出函数
,再经过求导分析得出函数 不存在“中值相依切线”.
不存在“中值相依切线”.试题解析:(1)函数
 的定义域是
的定义域是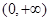 . 由已知得,
. 由已知得,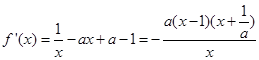
当
 时,
时, 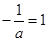 , 显然函数
, 显然函数 在
在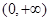 上单调递增;
上单调递增;当
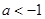 时,
时, 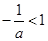 ,令
,令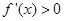 ,解得
,解得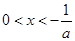 或
或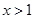 ;
;  函数
函数 在
在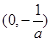 和
和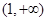 上单调递增,
上单调递增, 综上所述:①当
 时,函数
时,函数 在
在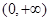 上单调递增;
上单调递增;②当
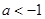 时,函数
时,函数 在
在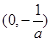 和
和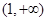 上单调递增;
上单调递增; (2)假设函数
 存在“中值相依切线”
存在“中值相依切线” 设
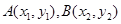 是曲线
是曲线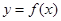 上的不同两点,且
上的不同两点,且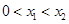 ,
,则
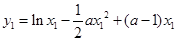 ,
,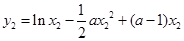 .
. 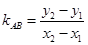
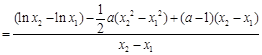

曲线在点
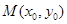 处的切线斜率
处的切线斜率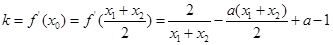
依题意得:
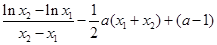

化简可得:
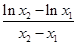
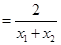 , 即
, 即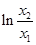 =
=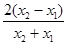
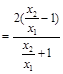
设
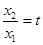 (
(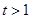 ),上式化为:
),上式化为: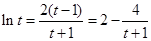 ,
, 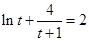 . 令
. 令 ,
, 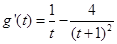
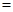
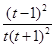 .
.因为
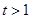 ,显然
,显然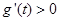 ,所以
,所以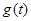 在
在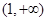 上递增,
上递增,显然有
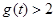 恒成立. 所以在
恒成立. 所以在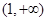 内不存在
内不存在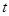 ,使得
,使得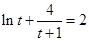 成立.
成立.综上所述,假设不成立.所以,函数
 不存在“中值相依切线”.
不存在“中值相依切线”.
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 在
在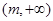 上为增函数(
上为增函数( 为常数),则称
为常数),则称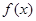 为区间
为区间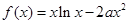 是
是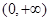 上的“一阶比增函数”,求实数
上的“一阶比增函数”,求实数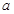 的取值范围;
的取值范围;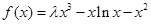 (
(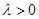 ,
,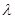 为常数),且
为常数),且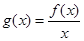 有唯一的零点,求
有唯一的零点,求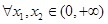 ,
,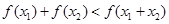
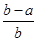 <ln
<ln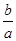 <
<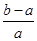 ,其中0<a<b;
,其中0<a<b;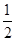 + +
+ +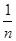 ]≤1+[lnn](n∈N*).
]≤1+[lnn](n∈N*).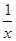 -1.
-1. 在区间
在区间 上有极值点,则实数
上有极值点,则实数 的取值范围是( )
的取值范围是( )



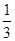 x3+ax2+bx(a,b∈R).
x3+ax2+bx(a,b∈R).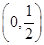 上不存在极值点,求a的取值范围.
上不存在极值点,求a的取值范围.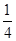
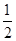
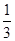 x3-2x2+3m,x∈[0,+∞),若f(x)+5≥0恒成立,则实数m的取值范围是________.
x3-2x2+3m,x∈[0,+∞),若f(x)+5≥0恒成立,则实数m的取值范围是________.