题目内容
16.对于正整数n,设曲线y=xn(1-x)在x=2的切线与平面直角坐标系的y轴交点的纵坐标为an,则数列$\{{log_2}\frac{a_n}{n+1}\}$的前10项等于55.分析 欲求数列$\{{log_2}\frac{a_n}{n+1}\}$的前10项和,必须求出在x=2处的切线方程,须求出其斜率的值即可,故先利用导数求出在x=2处的导函数值,再结合导数的几何意义即可求出切线的斜率即得直线方程进而得到切线与y轴交点的纵坐标.最后利用对数的运算性质和等差数列的求和公式计算,从而问题解决.
解答 解:y′=nxn-1-(n+1)xn,
曲线y=xn(1-x)在x=2处的切线的斜率为k=n•2n-1-(n+1)•2n,
切点为(2,-2n),
所以切线方程为y+2n=k(x-2),
令x=0得an=(n+1)2n,
令bn=log2$\frac{{a}_{n}}{n+1}$.
数列{bn}的前10项和为log22+log222+log223+…+log2210
=1+2+3+…+10=$\frac{1}{2}$×10×11=55.
故答案为:55.
点评 本题考查应用导数求曲线切线的斜率,数列通项公式以及等差数列的前n项和的公式.解后反思:应用导数求曲线切线的斜率时,要首先判定所经过的点为切点.否则容易出错.

练习册系列答案
相关题目
6.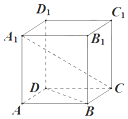 如图,四棱柱ABCD-A1B1C1D1的底面是菱形且D1D⊥平面ABCD,则A1C与BD所成的角是( )
如图,四棱柱ABCD-A1B1C1D1的底面是菱形且D1D⊥平面ABCD,则A1C与BD所成的角是( )
 如图,四棱柱ABCD-A1B1C1D1的底面是菱形且D1D⊥平面ABCD,则A1C与BD所成的角是( )
如图,四棱柱ABCD-A1B1C1D1的底面是菱形且D1D⊥平面ABCD,则A1C与BD所成的角是( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
1.设双曲线$\frac{x^2}{m}+\frac{y^2}{n}=1$的离心率为$\frac{{2\sqrt{3}}}{3}$,且一个焦点与抛物线x2=8y的焦点相同,则此双曲线的方程是( )
| A. | $\frac{y^2}{3}-{x^2}=1$ | B. | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | C. | ${y^2}-\frac{x^2}{3}=1$ | D. | $\frac{x^2}{12}-\frac{y^2}{4}=1$ |
8.若变量x,y满足约束条件$\left\{\begin{array}{l}y≤x\\ x+y≤1\\ y≥-1\end{array}\right.$,且z=2x+y的最大值和最小值分别为m和n,则m+n=( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
5.已知集合A={x|y=lg(x+1)},B=$\left\{{\left.x\right|\frac{3-x}{x}<0}\right\}$,则有( )
| A. | -3∈A | B. | A∩B=(-1,0) | C. | A∪B=R | D. | A?B |
6.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)与椭圆$\frac{{x}^{2}}{{m}^{2}}$$+\frac{4{y}^{2}}{{m}^{2}}$=1的离心率互为倒数,则双曲线的渐近线方程是( )
| A. | y=±$\frac{\sqrt{3}}{3}$x | B. | y=±$\frac{1}{3}$x | C. | y=±$\sqrt{3}$x | D. | y=$±\frac{\sqrt{3}}{2}$x |
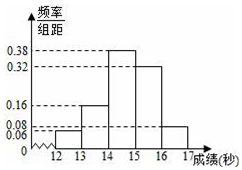 某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.
某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.