题目内容
已知函数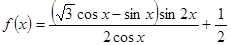 .
.
(I)求 的值;
的值;
(II)求函数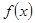 的最小正周期及单调递减区间.
的最小正周期及单调递减区间.
(Ⅰ) ;(Ⅱ)最小正周期为
;(Ⅱ)最小正周期为 ,单调递减区间为
,单调递减区间为 .
.
解析试题分析:(1)直接计算 的值,若式子的结果较复杂时,一般将函数解析式先化简再求值;(2)求函数
的值,若式子的结果较复杂时,一般将函数解析式先化简再求值;(2)求函数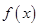 的最小正周期、单调区间等基本性质,一般先将函数解析式进行化简,即一般将三角函数解析式化为
的最小正周期、单调区间等基本性质,一般先将函数解析式进行化简,即一般将三角函数解析式化为 的形式,然后利用公式
的形式,然后利用公式 即可求出函数
即可求出函数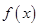 的最小正周期,利用复合函数法结合正弦函数的单调性即可求出函数
的最小正周期,利用复合函数法结合正弦函数的单调性即可求出函数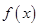 相应的单调区间,但首先应该求函数的定义域.
相应的单调区间,但首先应该求函数的定义域.
试题解析:解(Ⅰ)


 4分
4分
(Ⅱ)由
故 的定义域为
的定义域为
因为





所以 的最小正周期为
的最小正周期为
因为函数 的单调递减区间为
的单调递减区间为 ,
,
由
得
所以 的单调递减区间为
的单调递减区间为
13分
考点:三角函数的周期、单调区间、辅助角变换

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
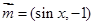 ,向量
,向量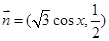 ,函数
,函数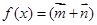 ·
·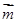 .
. 的最小正周期T;
的最小正周期T;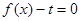 在
在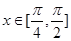 上有解,求实数
上有解,求实数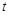 的取值范围.
的取值范围.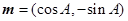 ,
,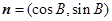 ,
,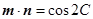 ,其中
,其中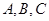 为
为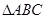 的内角.
的内角.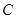 的大小;
的大小;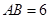 ,且
,且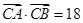 ,求
,求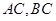 的长.
的长. ,
, ,
,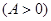 ,函数
,函数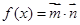 的最大值为
的最大值为 .
. ;
;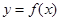 的图像向左平移
的图像向左平移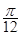 个单位,再将所得图像上各点的横坐标缩短为原来的
个单位,再将所得图像上各点的横坐标缩短为原来的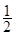 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数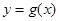 的图像,求
的图像,求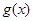 在
在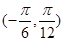 上的值域.
上的值域. ,
, ,
,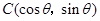 (
(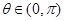 ),
),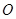 为坐标原点,向量
为坐标原点,向量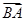 与向量
与向量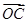 共线.
共线.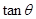 的值;
的值;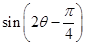 的值.
的值.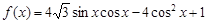 .
.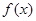 在
在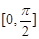 上的值域;
上的值域;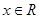 ,不等式
,不等式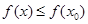 恒成立,求
恒成立,求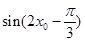 .
. 为第三象限角,
为第三象限角,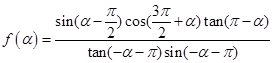 .
.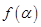 (2)若
(2)若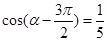 ,求
,求 ,
, .
. 的最大值和最小值;
的最大值和最小值; 在
在 的取值范围.
的取值范围.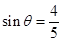 ,
,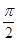 <θ<π.
<θ<π. 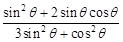 的值.
的值.