题目内容
设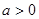 ,函数
,函数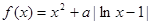
(1)当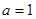 时,求曲线
时,求曲线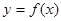 在
在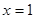 处的切线方程;
处的切线方程;
(2)当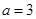 时,求函数
时,求函数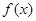 的单调区间;
的单调区间;
(3)当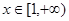 时,求函数
时,求函数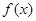 的最小值
的最小值
【答案】
(1) 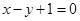 ;(2)
;(2)
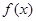 在
在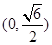 内单调递减,
内单调递减,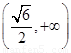 内单调递增;
内单调递增;
(3)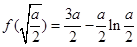
【解析】
试题分析:(1)写出函数的解析式,求导得斜率,求切点,进而得直线方程,注意解析式的取舍( 时);(2)函数为分段函数,分段判单调性,求出函数的单调区间;(3)分
时);(2)函数为分段函数,分段判单调性,求出函数的单调区间;(3)分 和
和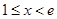 两种情况进行分析,在第二种情况下要对
两种情况进行分析,在第二种情况下要对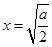 与区间
与区间 进行比较,又分三种情况进行判断单调性,求最小值
进行比较,又分三种情况进行判断单调性,求最小值
试题解析:(1)当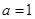 时,
时,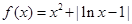 ,令
,令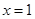 得
得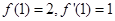 ,
,
所以切点为 ,切线斜率为1,
,切线斜率为1,
所以曲线 在
在 处的切线方程为:
处的切线方程为: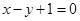
(2)当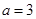 时
时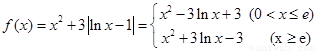
当 时,
时,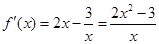 ,
,
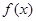 在
在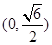 内单调递减,
内单调递减, 内单调递增;
内单调递增;
当 时,
时,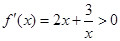 恒成立,故
恒成立,故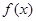 在
在 内单调递增;
内单调递增;
综上,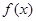 在
在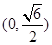 内单调递减,
内单调递减,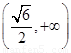 内单调递增.
内单调递增.
(3)①当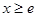 时,
时,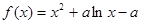 ,
,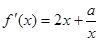
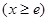
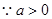 ,
,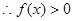 恒成立.
恒成立. 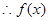 在
在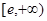 上增函数.
上增函数.
故当 时,
时,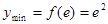
② 当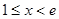 时,
时,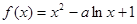 ,
,
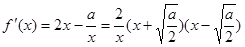 (
(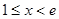 )
)
ⅰ)当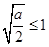 ,即
,即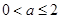 时,
时,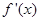 在
在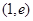 时为正数,所以函数
时为正数,所以函数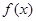 在
在 上为增函数,
上为增函数,
故当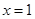 时,
时,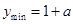 ,且此时
,且此时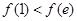
ⅱ)当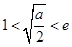 ,即
,即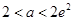 时,
时,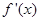 在
在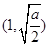 时为负数,在
时为负数,在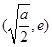 时为正数,
时为正数,
所以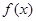 在
在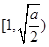 上为减函数,在
上为减函数,在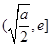 为增函数
为增函数
故当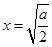 时,
时, ,且此时
,且此时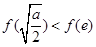
ⅲ)当 ,即
,即 时,
时,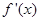 在
在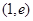 时为负数,所以函数
时为负数,所以函数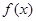 在
在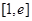 上为减函数,
上为减函数,
故当 时,
时,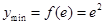
综上所述,当 时,函数
时,函数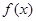 在
在 和
和 时的最小值都是
时的最小值都是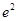
所以此时函数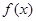 的最小值为
的最小值为 ;当
;当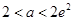 时,函数
时,函数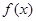 在
在 时的最小值为
时的最小值为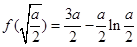 ,而
,而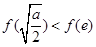 ,
,
所以此时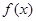 的最小值为
的最小值为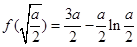
考点:1 求切线方程;2 函数的单调性判断(导数法);3 利用导数求函数的最值

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
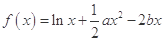 .
. ,
,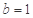 时,求函数
时,求函数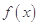 的最大值;
的最大值;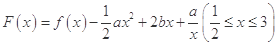 ,其图象上存在一点
,其图象上存在一点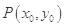 ,使此处切线的斜率
,使此处切线的斜率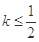 ,求实数
,求实数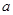 的取值范围;
的取值范围;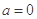 ,
,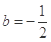 时,方程
时,方程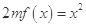 有唯一实数解,求正数
有唯一实数解,求正数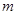 的值.
的值.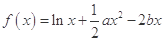 .
.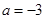 ,
,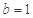 时,求函数
时,求函数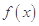 的最大值;
的最大值;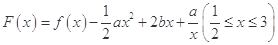 ,其图象上存在一点
,其图象上存在一点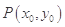 ,使此处切线的斜率
,使此处切线的斜率 ,求实数
,求实数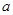 的取值范围;
的取值范围;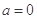 ,
,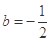 ,
,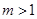 时,方程
时,方程 有唯一实数解,求
有唯一实数解,求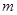 的值.
的值.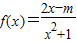
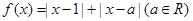
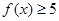 的解集
的解集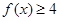 对
对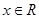 恒成立,求a的取值范围。
恒成立,求a的取值范围。