题目内容
选修4—5：不等式选讲
设函数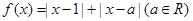
（1）当a=4时，求不等式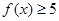
的解集
（2）若
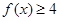对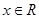
恒成立，求a的取值范围。
【答案】
(Ⅰ) 
或
． (Ⅱ) 
或
．
【解析】本试题主要是考查了绝对值不等式的求解，以及不等式恒成立问题的运用。
（1）利用零点分段论的思想，进行分析函数，然后各段求解不等式得到解集。
（2）利用不等式
对
恒成立，只要求解函数的最小值即可。
运用距对峙的几何意义得到最小值，从而得到参数的范围。
解:(Ⅰ)
等价于
或
或
，
解得：
或
．
故不等式
的解集为或．
……5分
(Ⅱ)因为: 
（当
时等号成立）
所以：
……8分
由题意得：
，
解得或．
……10分
练习册系列答案
阅读快车系列答案
相关题目