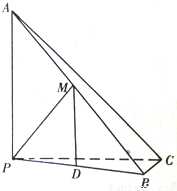
题目内容
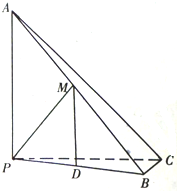
 已知三棱锥A-PBC,∠ACB=90°,AB=20,BC=4,PA⊥PC,D为AB边中点且△PDB为正三角形.
已知三棱锥A-PBC,∠ACB=90°,AB=20,BC=4,PA⊥PC,D为AB边中点且△PDB为正三角形.(1)求证:BC⊥平面PAC;
(2)求三棱锥D-PBC的体积.
分析:(1)由D为AB边中点且△PDB为正三角形可得AP⊥PB,结合PA⊥PC及线面垂直的判定定理可得PA⊥平面PBC,进而PA⊥BC,由∠ACB=90°结合线面垂直的判定定理可得BC⊥平面PAC;
(2)由AB=20,BC=4,D为AB边中点结合(1)中结论,求出三棱锥D-PBC的底面积和高,代入棱锥体积公式,可得答案.
(2)由AB=20,BC=4,D为AB边中点结合(1)中结论,求出三棱锥D-PBC的底面积和高,代入棱锥体积公式,可得答案.
解答:证明:(1)∵D为AB边中点且△PDB为正三角形
∴AP⊥PB
又∵PA⊥PC,PB∩PC=B,PB,PC?平面PBC
∴PA⊥平面PBC
又∵BC?平面PBC
∴PA⊥BC
∵∠ACB=90°,
∴AC⊥BC
又∵PA∩AC=A,PA,AC?平面PAC
∴BC⊥平面PAC;
解:(2)在Rt△PAB中,AB=20,PB=
AB=10
∴PA=
=10
∵D为AB边中点
∴三棱锥D-PBC的高h=
PA=5
底面PBC中,BC=4,
∴PC=
=2
故S△PBC=
•PC•BC=4
故三棱锥D-PBC的体积V=
•S△PBC•h=20
∴AP⊥PB
又∵PA⊥PC,PB∩PC=B,PB,PC?平面PBC
∴PA⊥平面PBC
又∵BC?平面PBC
∴PA⊥BC
∵∠ACB=90°,
∴AC⊥BC
又∵PA∩AC=A,PA,AC?平面PAC
∴BC⊥平面PAC;
解:(2)在Rt△PAB中,AB=20,PB=
| 1 |
| 2 |
∴PA=
| AB2-PB2 |
| 3 |
∵D为AB边中点
∴三棱锥D-PBC的高h=
| 1 |
| 2 |
| 3 |
底面PBC中,BC=4,
∴PC=
| PB2-BC2 |
| 21 |
故S△PBC=
| 1 |
| 2 |
| 21 |
故三棱锥D-PBC的体积V=
| 1 |
| 3 |
| 7 |
点评:本题考查的知识点是直线与平面垂直的判定,棱锥的体积,熟练掌握空间线线垂直与线面垂直之间的转化关系是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
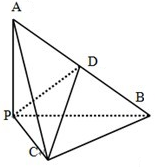
 如图,已知三棱锥A-PBC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且AB=2MP.
如图,已知三棱锥A-PBC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且AB=2MP. PC,D为AB中点且△PDB为正三角形
PC,D为AB中点且△PDB为正三角形