题目内容
如图，已知三棱锥A-PBC中，AP⊥PC，AC⊥BC，M为AB中点，D为PB中点，且AB=2MP．
（1）求证：DM∥平面APC；
（2）求证：平面ABC⊥平面APC．
（1）求证：DM∥平面APC；
（2）求证：平面ABC⊥平面APC．
（1）由于M为AB中点，D为PB中点，故MD为三角形PAB的中位线，故MD∥AP．
而AP?平面APC，MD不在平面APC内，故有DM∥平面APC．
（2）∵M为AB中点，且AB=2MP，故有MA=MB=MP，故M为△PAB的外心，故有PA⊥PB．
再由AP⊥PC，PB∩PC=P，可得PA⊥平面PBC，故PA⊥BC．
再由BC⊥PC，PA∩PC=P，可得BC⊥平面PAC．
而BC?平面ABC，故有平面ABC⊥平面APC．
而AP?平面APC，MD不在平面APC内，故有DM∥平面APC．
（2）∵M为AB中点，且AB=2MP，故有MA=MB=MP，故M为△PAB的外心，故有PA⊥PB．
再由AP⊥PC，PB∩PC=P，可得PA⊥平面PBC，故PA⊥BC．
再由BC⊥PC，PA∩PC=P，可得BC⊥平面PAC．
而BC?平面ABC，故有平面ABC⊥平面APC．
练习册系列答案
阅读快车系列答案
相关题目
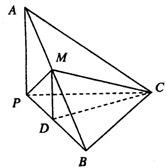如图，已知三棱锥A-BPC中，AP⊥PC，AC⊥BC，M为AB中点，D为PB中点，且△PMB为正三角形．
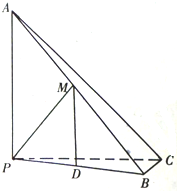如图，已知三棱锥A-PBC中，AP⊥PC，AC⊥BC，M为AB中点，D为PB中点，且AB=2MP．
如图，已知三棱锥A-BCD的棱长都相等，E，F分别是棱AB，CD的中点，则EF与BC所成的角是（ ）
如图，已知三棱锥A-BPC中，AP⊥PC，AC⊥BC，M为AB的中点，D为PB的中点，且△PMB为正三角形．