题目内容
设函数![]() 的定义域为
的定义域为![]() ,当
,当![]() 时,
时,![]() ,且对任意的实数
,且对任意的实数![]() ,有
,有![]() .
.
⑴求![]() ,判断并证明函数
,判断并证明函数![]() 的单调性;
的单调性;
⑵数列![]() 满足
满足![]() ,且
,且![]()
①求![]() 通项公式;
通项公式;
②当![]() 时,不等式
时,不等式![]() 对不小于
对不小于![]() 的正整数恒成立,求
的正整数恒成立,求![]() 的取值范围.
的取值范围.
⑴![]() ,⑵①
,⑵①![]() ,②
,②![]() 的取值范围是
的取值范围是![]()
解析:
从已知得到递推关系式,再由等差数列的定义入手;恒成立问题转化为左边的最小值. ⑴![]() ,
,![]() 在
在![]() 上减函数(解法略)
上减函数(解法略)
⑵ ①![]() 由
由![]() 单调性
单调性
![]() ,故
,故![]() 等差数列
等差数列
![]() ②
②![]()
![]()
![]() 是递增数列
是递增数列
当![]() 时,
时,![]()
![]()
![]() , 即
, 即![]()
而![]() ,∴
,∴![]() ,故
,故![]() 的取值范围是
的取值范围是![]()
【名师指引】数列与函数、方程、不等式的综合问题,要注意将其分解为数学分支中的问题来解决.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,求实数
,求实数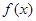 的定义域为
的定义域为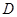 ,若存在非零常数
,若存在非零常数 使得对于任意
使得对于任意 有
有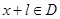 且
且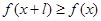 ,则称
,则称 上的
上的 的奇函数
的奇函数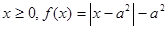 ,若
,若 的取值范围为________.
的取值范围为________.