题目内容
设
,函数
的定义域为
,且
,当
,有
；函数
是定义在
上单调递增的奇函数.
(Ⅰ)求
和
的值(用
表示);
(Ⅱ)求的值;
(Ⅲ)当
时, 
对所有的
均成立,求实数
的取值范围.
(Ⅰ) 
(Ⅱ) 
(Ⅲ)
解析:
解(Ⅰ) 因为当,有
所以,令
-----------2分
所以,令
---------4分
(Ⅱ) 令
令
------6分
所以
或
或
----------8分
(Ⅲ)
因为是定义在上单调递增的奇函数,所以
--------9分
令
----------10分
原题等价于“对于任意
，
恒成立” -------10分
令函数
所以对称轴
①当
时，只需满足
（舍去）------11分
②当
时，只需满足----------12分
，以
③当
时，只需满足
所以
---13分
综上所述：--------------14分
（本题(Ⅲ)还可以用分离变量法或数形结合，其它方法酌情给分）
练习册系列答案
相关题目
的定义域为
，当
时，
，且对于任意的实数
、
，都有
．（1）求
；（2）试判断函数
上是否存在最小值，若存在，求该最小值；若不存在，说明理由；（3）设数列
各项都是正数，且满足
，
（
），又设
，
，
， 当
时，试比较
与
的大小，并说明理由．
的定义域为D，若存在非零实数
使得对于任意
，有
，且
，则称
为R上的1高调函数；
为R上的
高调函数；
的函数
为
高调函数，那么实数
；
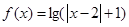为
上的2高调函数。
的定义域为R+，若对于给定的正数
，定义函数
则当函数
,
时，
的值为（ ）
B．
C．
D．
的定义域为R+，若对于给定的正数K，定义函数
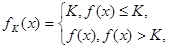，则当函数
时，定积分
的值为