题目内容
在直径为1的圆O中,作一关于圆心对称、邻边互相垂直的十字形,其中y>x>0.
(Ⅰ)将十字形的面积表示为θ的函数;
(Ⅱ)θ为何值时,十字形的面积最大?最大面积是多少?
(1)设S为十字形的面积,则S=2xy-x2=2sinθcosθ-cos2θ( <θ<
<θ<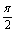 )
)
(2)解法1
S=2sinθcosθ-cos2θ=sin2θ- cos2θ
cos2θ ,其中
,其中 =1,即2θ-
=1,即2θ-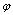 =
=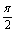 时,S最大.
时,S最大.
∴当θ= 时,S最大,S的最大值为
时,S最大,S的最大值为 .
.
解法2 ∵S=2sinθcosθ-cos2θ,
∴S′=2cos2θ- 2sin2θ+2sinθ·cosθ=2cos2θ+sin2θ.
令S′=0.即2cos2θ+sin2θ=0,
可解得θ= arctan(-2).
arctan(-2).
∴当θ= arctan(-2)时,S最大,S的最大值为
arctan(-2)时,S最大,S的最大值为 .
.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目

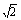 cosx的图像,只需将函数y=
cosx的图像,只需将函数y= 横坐标缩短到原来的
横坐标缩短到原来的 个单位长度
个单位长度  ,cos2x=a,则sinx ( )
,cos2x=a,则sinx ( )  B.-
B.- D.
D.  (
( )=1,则常数a,b的值为 ( )
)=1,则常数a,b的值为 ( ) -2,b=4 B.a=2,b=-4
-2,b=4 B.a=2,b=-4 与直线
与直线 ,直线
,直线 分别交于
分别交于 两点,
两点, 中点为
中点为 ,则直线
,则直线 B、
B、 C、
C、 D、
D、