题目内容
函数f（x）的图象与g（x）=（
）x的图象关于直线y=x对称，则f（2x-x2）的单调递减区间为________．
（0，1]
分析：由已知中函数f（x）的图象与g（x）=（）x的图象关于直线y=x对称，可得函数f（x）与g（x）=（）x互为反函数，由此易得到函数f（x）的解析式，结合复合函数同增异减的原则，即可得到f（2x-x2）的单调递减区间．
解答：因为f（x）与g（x）互为反函数，所以f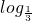（x）=
x
则f（2x-x2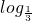）=（2x-x2），
令μ（x）=2x-x2＞0，解得0＜x＜2．
μ（x）=2x-x2在（0，1）上单调递增，
则f[μ（x）]在（0，1）上单调递减；
μ（x）=2x-x2在（1，2）上单调递减，
则f[μ（x）]在[1，2）上单调递增．
所以f（2x-x2）的单调递减区间为（0，1]
故答案为：（0，1]
点评：本题考查的知识点是反函数，根据互为反函数的图象关于直线y=x对称，及同底数的指数函数和对数互为反函数求出函数f（x）的解析式，是解答本题的关键．
分析：由已知中函数f（x）的图象与g（x）=（
）x的图象关于直线y=x对称，可得函数f（x）与g（x）=（）x互为反函数，由此易得到函数f（x）的解析式，结合复合函数同增异减的原则，即可得到f（2x-x2）的单调递减区间．解答：因为f（x）与g（x）互为反函数，所以f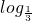（x）=
x则f（2x-x2）=
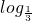（2x-x2），令μ（x）=2x-x2＞0，解得0＜x＜2．
μ（x）=2x-x2在（0，1）上单调递增，
则f[μ（x）]在（0，1）上单调递减；
μ（x）=2x-x2在（1，2）上单调递减，
则f[μ（x）]在[1，2）上单调递增．
所以f（2x-x2）的单调递减区间为（0，1]
故答案为：（0，1]
点评：本题考查的知识点是反函数，根据互为反函数的图象关于直线y=x对称，及同底数的指数函数和对数互为反函数求出函数f（x）的解析式，是解答本题的关键．
练习册系列答案
相关题目