题目内容
已知△ABC中,AB=1,BC=2,求角C的取值范围.
解:设AC=x.
则![]() 即1<x<3,据余弦定理:x2+4-4xcosC=1,即x2-4cosC·x+3=0.
即1<x<3,据余弦定理:x2+4-4xcosC=1,即x2-4cosC·x+3=0.
关于x的一元二次方程在(1,3)之间有解,则令f(x)=x2-4cosC·x+3,有f(1)f(3)<0,①
或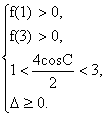 ②
②
解①得48(1-cosC)2<0,无解.
解②得cosC≥![]() .
.
又0<C<π,
∴0<C≤![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
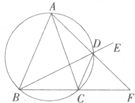 已知△ABC中AB=AC,D为△ABC外接圆劣弧,
已知△ABC中AB=AC,D为△ABC外接圆劣弧,
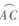 上的点(不与点A、C重合),延长BD至E,延长交BC的延长线于F .
上的点(不与点A、C重合),延长BD至E,延长交BC的延长线于F .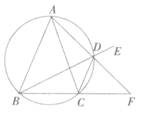
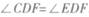 ;
;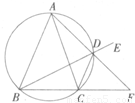 已知△ABC中AB=AC,D为△ABC外接圆劣弧,
已知△ABC中AB=AC,D为△ABC外接圆劣弧,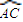 上的点(不与点A、C重合),延长BD至E,延长AD交BC的延长线于F.
上的点(不与点A、C重合),延长BD至E,延长AD交BC的延长线于F.