题目内容
已知△ABC中AB=4，AC=5，BC=7，点O是其内切圆圆心，则
•
= ．
| AO |
| BC |
分析：利用三角形的内切圆的性质、向量的运算和数量积运算性质即可得出．
解答：解：如图所示，
设点D，E，F分别是内切圆与三边相切的切点．
设AE=AF=x，CE=CD=y，BD=BF=z．
则
，解得x=1．
设∠DAC=θ．在Rt△OAE中，AO•cosθ=AE=1．
∴
•
=
•(
-
)=
•
-
•
=|
| |
|cosθ-|
| |
|cosθ
=5|
|cosθ-4|
|cosθ
=|
|cosθ
=1．
故答案为：1．
设点D，E，F分别是内切圆与三边相切的切点．
设AE=AF=x，CE=CD=y，BD=BF=z．
则
|
设∠DAC=θ．在Rt△OAE中，AO•cosθ=AE=1．
∴
| AO |
| BC |
| AO |
| AC |
| AB |
| AO |
| AB |
| AO |
| AC |
| AO |
| AB |
| AO |
| AC |
=5|
| AO |
| AO |
=|
| AO |
=1．
故答案为：1．
点评：本题考查了三角形的内切圆的性质、向量的运算和数量积运算性质，属于难题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
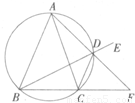
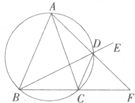已知△ABC中AB=AC，D为△ABC外接圆劣弧，
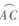上的点(不与点A、C重合），延长BD至E，延长交BC的延长线于F .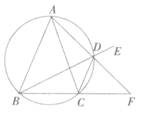
；
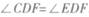已知△ABC中AB=AC，D为△ABC外接圆劣弧，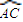
上的点（不与点A、C重合），延长BD至E，延长AD交BC的延长线于F．