题目内容
【题目】在直角坐标系xOy中，直线l的参数方程为 
（t为参数，α为直线的倾斜角）．以平面直角坐标系xOy极点，x的正半轴为极轴，取相同的长度单位，建立极坐标系．圆的极坐标方程为ρ=2cosθ，设直线与圆交于A，B两点． （Ⅰ）求圆C的直角坐标方程与α的取值范围；
（Ⅱ）若点P的坐标为（﹣1，0），求 
+ 
取值范围．
【答案】解：（Ⅰ）∵圆的极坐标方程为ρ=2cosθ， ∴圆C的直角坐标方程x2+y2﹣2x=0，
把 
代入x2+y2﹣2x=0，得t2﹣4tcosα+3=0，
又直线l与圆C交于A，B两点，∴△=16cos2α﹣12＞0，
解得： 
或 
又由α∈[0，π），故α的取值范围 
．
（Ⅱ）设方程t2﹣4tcosα+3=0的两个实数根分别为t1 ， t2 ，
则由参数t的几何意义可知： 
，
又由 
，∴ 
，
∴ 
的取值范围为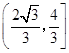 
．
【解析】（Ⅰ）由圆的极坐标方程，能求出圆C的直角坐标方程，把 
代入x2+y2﹣2x=0，得t2﹣4tcosα+3=0，由此利用根的判别式能求出α的取值范围． （Ⅱ）设方程t2﹣4tcosα+3=0的两个实数根分别为t1 ， t2 ， 则由参数t的几何意义可知： 
，由此能求出 
的取值范围．
【题目】近年来，共享单车已经悄然进入了广大市民的日常生活，并慢慢改变了人们的出行方式.为了更好地服务民众，某共享单车公司在其官方
中设置了用户评价反馈系统，以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出
条较为详细的评价信息进行统计，车辆状况的优惠活动评价的
列联表如下：
对优惠活动好评 | 对优惠活动不满意 | 合计 | |
对车辆状况好评 |
|
|
|
对车辆状况不满意 |
|
|
|
合计 |
|
|
|
（1）能否在犯错误的概率不超过
的前提下认为优惠活动好评与车辆状况好评之间有关系？
（2）为了回馈用户，公司通过向用户随机派送每张面额为
元，元，
元的 三种骑行券.用户每次使用扫码用车后，都可获得一张骑行券.用户骑行一次获得
元券，获得元券的概率分别是
，
，且各次获取骑行券的结果相互独立.若某用户一天使用了两次该公司的共享单车，记该用户当天获得的骑行券面额之和为
，求随机变量的分布列和数学期望.
参考数据：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式：
，其中
.
