Question

【题目】已知椭圆的离心率为，以原点O为圆心，椭圆C的长半轴长为半径的圆与直线相切.

⑴求椭圆C的标准方程；

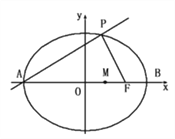
⑵已知点A、B为动直线与椭圆C的两个交点，问：在x轴上是否存在定点E，使得为定值？若存在，试求出点E的坐标和定值；若不存在，请说明理由.

Answer 1

【答案】（1）（2）定值为

【解析】试题分析：（Ⅰ）由e=，以原点O为圆心，椭圆C的长半轴长为半径的圆与直线相切，求出a，b，由此能求出椭圆的方程．

（Ⅱ）由，得（1+3k2）x2﹣12k2x+12k2﹣6=0，由此利用韦达定理、向量的数量积，结合已知条件能求出在x轴上存在点E，使为定值，定点为（）．

试题解析：

（Ⅰ）由e=，得=，即c=a，①

以原点O为圆心，椭圆C的长半轴长为半径的圆为x2+y2=a2，

此圆与直线2x﹣+6=0相切，∴a==，

代入①得c=2，（4分）

∴b2=a2﹣c2=2，∴椭圆的方程为．

（Ⅱ）由，得（1+3k2）x2﹣12k2x+12k2﹣6=0，（6分）

设A（x1，y1），B（x2，y2），∴，，

根据题意，假设x轴上存在定点E（m，0），使得为定值，

则有=（x1﹣m，y1）（x2﹣m，y2）=（x1﹣m）（x2﹣m）+y1y2

=

=（k2+1）

=（k2+1）﹣（2k2+m）+（4k2+m2）

=，

要使上式为定值，即与k无关，则应有3m2﹣12m+10=3（m2﹣6），

即m=，此时=为定值，定点为（）．