题目内容
设不等式 的解集为
的解集为 .
.
(1)求集合 ;
;
(2)设关于 的不等式
的不等式 的解集为
的解集为 ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围.
(1)A={x|1≤x≤4}(2) 的取值范围为
的取值范围为 .
.
解析试题分析:(1)求出不等式x2≤5x-4的解集确定出集合A,
(2)若B⊆A,求实数m的取值范围进要注意B是空集的情况,故此题分为两类求,是空集时,不是空集时,比较两个集合的端点即可.
试题解析:(1)原不等式即为x2-5x+4=(x-1)(x-4)≤0,所以1≤x≤4,
所以不等式的解集A={x|1≤x≤4}.
(2)原不等式等价于
若 ,则
,则 ,要
,要 ,只需
,只需
若 ,则
,则 ,要
,要 ,只需
,只需
若 ,则
,则 ,符合
,符合
综上所述, 的取值范围为
的取值范围为 .
.
考点:一元二次不等式的解法;集合中的参数取值问题;集合包含关系的判断.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
 ,
, ,
, ,
, = 。
= 。 },B={x|x2﹣5x﹣6<0,
},B={x|x2﹣5x﹣6<0,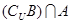 .
.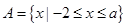 ,
,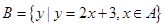 ,
,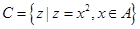 ,且
,且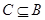 ,求
,求 的取值范围.
的取值范围.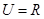 ,集合
,集合
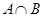 (2)求
(2)求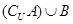
 集合
集合 .
. ,求
,求 ;
; ,求实数
,求实数 的取值范围.
的取值范围. ,
, .
. ,
, ,且
,且 ,求
,求
 ,
, ,且
,且 ,则
,则 的取值组成的集合是______ .
的取值组成的集合是______ .