题目内容
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)若![]() 是函数
是函数![]() 的极值点,求
的极值点,求![]() 的值;
的值;
(Ⅱ)若![]() 在区间
在区间![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】
试题分析:(I)由![]() ,得
,得![]() ,根据
,根据![]() 是函数
是函数![]() 的极值点,即可求解实数
的极值点,即可求解实数![]() 的值;(II)由
的值;(II)由![]() 在区间
在区间![]() 上单调递增,得
上单调递增,得![]() 在区间
在区间![]() 上恒成立,得到
上恒成立,得到![]() 对区间
对区间![]() 恒成立,设
恒成立,设![]() ,利用导数求解函数
,利用导数求解函数![]() 的最小值,即可求解实数
的最小值,即可求解实数![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)由![]() ,得
,得![]() ,………………2分
,………………2分
∵![]() 是函数
是函数![]() 的极值点,
的极值点,
∴ ![]() ,解得
,解得![]() ,………4分
,………4分
经检验![]() 为函数,
为函数,![]() 的极值点,(不检验1分扣去)
的极值点,(不检验1分扣去)
所以![]() .……………5分
.……………5分
(Ⅱ)∵![]() 在区间
在区间![]() 上单调递增,
上单调递增,
∴![]() 在区间
在区间![]() 上恒成立,
上恒成立,
∴![]() 对区间
对区间![]() 恒成立,………8分
恒成立,………8分
令![]() ,则
,则![]()
∴当![]() 时,
时,![]() ,有
,有![]() ……………12分
……………12分
∴![]() 的取值范围为
的取值范围为![]() …………13分
…………13分
法二:上同,
∴![]() 对区间
对区间![]() 恒成立,………………8分
恒成立,………………8分
令![]() ,
,![]() ,则
,则![]() ,
,![]()
∴![]() ,
,![]()
∵![]() ,在
,在![]() 上单调递增函数
上单调递增函数
∴![]() ………………12分
………………12分
∴![]() 的取值范围为
的取值范围为![]() ………………13分
………………13分
法三:∵![]() 在区间
在区间![]() 上单调递增,
上单调递增,
∴![]() 在区间
在区间![]() 上恒成立,………………8分
上恒成立,………………8分
记![]() ,则
,则
![]() 或
或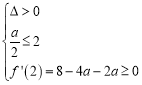
即![]() 或
或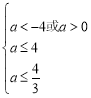
解得![]() ………………12分
………………12分
∴![]() 的取值范围为
的取值范围为![]() ……………13分
……………13分

练习册系列答案
相关题目