题目内容
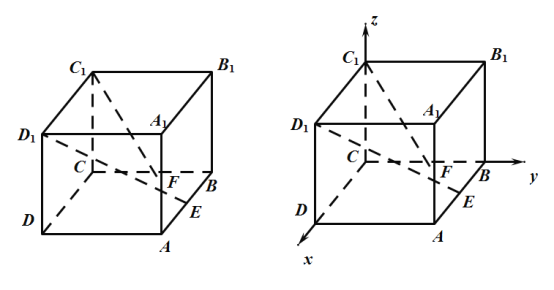
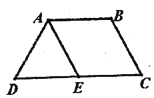
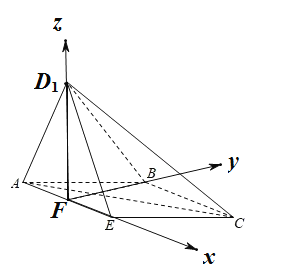
【题目】如图,等腰梯形![]() 中,
中,![]()
![]() ,
,![]() ,E为CD中点,将
,E为CD中点,将![]() 沿AE折到
沿AE折到![]() 的位置.
的位置.
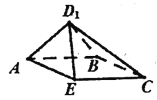
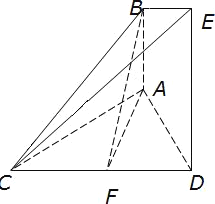
(1)证明:![]() ;
;
(2)当折叠过程中所得四棱锥![]() 体积取最大值时,求直线
体积取最大值时,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析
(2)![]()
【解析】
(1)在平面图中,连BE,DB,设DB交AE于F,要证![]() ,转证
,转证![]() 平面
平面![]() ,即证
,即证![]()
![]() ;
;
(2)要使四棱锥体积最大,则需要平面![]() 垂直于底面
垂直于底面![]() ,以
,以![]() 为原点建立直角坐标系,利用空间向量法求出线面角的正弦值.
为原点建立直角坐标系,利用空间向量法求出线面角的正弦值.
解:(1)在平面图中,连BE,DB,设DB交AE于F,
因为![]() 是等腰梯形,
是等腰梯形,![]()
![]() ,
,![]() ,E为CD中点
,E为CD中点
![]()
即![]() ,且
,且![]()
故四边形![]() 为平行四边形
为平行四边形
又![]()
所以平行四边形![]() 为棱形,
为棱形,
同理可证![]() 也为棱形
也为棱形
所以![]() .
.
于是得出在立体图形中,![]()
![]()
![]() ,
,![]() 平面
平面![]()
所以![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
故![]()

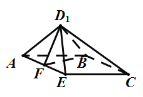
(2)要使四棱锥体积最大,则需要平面![]() 垂直于底面
垂直于底面![]() ,
,
此时![]() 平面
平面![]() ,
,
以![]() 为原点,
为原点,![]() 为
为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
则![]()
则![]()
设平面![]() 的法向量为
的法向量为![]()
由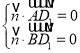 ,得
,得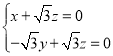
令![]() ,得
,得![]()
![]()
![]() 直线
直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
【题目】某高中三年级有AB两个班,各有50名同学,这两个班参加能力测试,成绩统计结果如表:
AB班成绩的频数分布表
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
A班频数 | 4 | 8 | 23 | 9 | 6 |
B班频数 | 7 | 12 | 13 | 10 | 8 |
(1)试估计AB两个班的平均分;
(2)统计学中常用M值作为衡量总体水平的一种指标,已知M与分数t的关系式为:M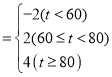 .
.
分别求这两个班学生成绩的M总值,并据此对这两个班的总体水平作简单评价.