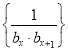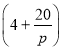题目内容
【题目】对于双曲线![]() :
:![]() (
(![]() ),若点
),若点![]() 满足
满足![]() ,则称
,则称![]() 在
在![]() 的外部;若点
的外部;若点![]() 满足
满足![]() ,则称
,则称![]() 在
在![]() 的内部.
的内部.
(1)证明:直线![]() 上的点都在
上的点都在![]() 的外部.
的外部.
(2)若点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 的内部或
的内部或![]() 上,求
上,求![]() 的最小值.
的最小值.
(3)若![]() 过点
过点![]() ,圆
,圆![]() (
(![]() )在
)在![]() 内部及
内部及![]() 上的点构成的圆弧长等于该圆周长的一半,求
上的点构成的圆弧长等于该圆周长的一半,求![]() 、
、![]() 满足的关系式及
满足的关系式及![]() 的取值范围.
的取值范围.
【答案】(1)见解析 (2) 最小值为![]() .(3)
.(3) ![]() ,
,![]() 的取值范围为
的取值范围为![]() .
.
【解析】
(1)设直线上的点坐标为![]() ,代入双曲线
,代入双曲线![]() 方程检验;
方程检验;
(2)设点![]()
![]() ,由题设
,由题设![]() .
.![]() ,求得这个式子的最小值即可.
,求得这个式子的最小值即可.
(3)由于圆![]() 和双曲线
和双曲线![]() 均关于坐标轴和原点对称,所以只需考虑这两个曲线在第一象限及
均关于坐标轴和原点对称,所以只需考虑这两个曲线在第一象限及![]() 、
、![]() 轴正半轴的情况.圆与双曲线的交点平分该圆在第一象限内的圆弧,它们交点的坐标为
轴正半轴的情况.圆与双曲线的交点平分该圆在第一象限内的圆弧,它们交点的坐标为 .代入双曲线方程得
.代入双曲线方程得![]() (*),双曲线过点
(*),双曲线过点![]() ,得
,得![]() ,消去
,消去![]() 得
得![]() .
.
由![]() 得
得![]() 的取值范围.
的取值范围.
(1)设直线![]() 上点的坐标为
上点的坐标为![]() ,代入
,代入![]() ,
,
得![]() ,
,
对于![]() ,
,![]() ,因此,直线
,因此,直线![]() 上的点都在
上的点都在![]() 的外部.
的外部.
(2)设点![]() 的坐标为
的坐标为![]() ,由题设
,由题设![]() .
.
![]() ,由
,由![]() ,得
,得![]() ,
,
对于![]() ,有
,有![]() ,于是
,于是![]() ,
,
因此,![]() 的最小值为
的最小值为![]() .
.
(3)因为圆![]() 和双曲线
和双曲线![]() 均关于坐标轴和原点对称,所以只需考虑这两个曲线在第一象限及
均关于坐标轴和原点对称,所以只需考虑这两个曲线在第一象限及![]() 、
、![]() 轴正半轴的情况.
轴正半轴的情况.
由题设,圆与双曲线的交点平分该圆在第一象限内的圆弧,它们交点的坐标为 .…
.…
将![]() ,
,![]() 代入双曲线
代入双曲线![]() 方程,得
方程,得![]() (*),
(*),
又因为![]() 过点
过点![]() ,所以
,所以![]() ,
,
将![]() 代入(*)式,得
代入(*)式,得![]() .
.
由![]() ,解得
,解得![]() .因此,
.因此,![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目