题目内容
已知椭圆C的中心在坐标原点,焦点在x轴上,它的一个顶点恰好是抛物线 的焦点,离心率为
的焦点,离心率为 .
.
(1)求椭圆C的标准方程;
(2)过椭圆C的右焦点F作直线l交椭圆C于A、B两点,交y轴于M点,若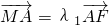 ,
,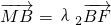 ,求证:λ1+λ2=-10.
,求证:λ1+λ2=-10.
解:(1)解:设椭圆C的方程为 (a>b>0),
(a>b>0),
抛物线方程化为x2=4y,其焦点为(0,1)
则椭圆C的一个顶点为(0,1),即b=1
由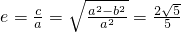 ,∴a2=5,
,∴a2=5,
所以椭圆C的标准方程为
(2)证明:易求出椭圆C的右焦点F(2,0),
设A(x1,y1),B(x2,y2),M(0,y0),显然直线l的斜率存在,
设直线l的方程为y=k(x-2),代入方程 并整理,
并整理,
得(1+5k2)x2-20k2x+20k2-5=0
∴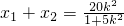 ,
,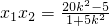
又,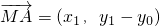 ,
, ,
,
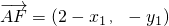 ,
,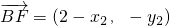 ,而
,而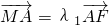 ,
,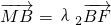 ,
,
即(x1-0,y1-y0)=λ1(2-x1,-y1),(x2-0,y2-y0)=λ2(2-x2,-y2)
∴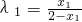 ,
,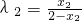 ,
,
所以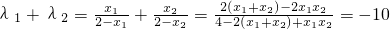
分析:(1)设出椭圆的方程,把抛物线方程整理成标准方程,求得焦点的坐标,进而求得椭圆的一个顶点,即b,利用离心率求得a和c关系进而求得a,则椭圆的方程可得.
(2)先根据椭圆的方程求得右焦点,设出A,B,M的坐标设出直线l的方程代入椭圆方程整理后利用韦达定理表示出x1+x2和x1x2,进而根据 ,
, ,
, 和
和 利用题设条件求得λ1和λ2的表达式,进而求得λ1+λ2.
利用题设条件求得λ1和λ2的表达式,进而求得λ1+λ2.
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生综合分析问题的能力,知识的迁移能力以及运算能力.
 (a>b>0),
(a>b>0),抛物线方程化为x2=4y,其焦点为(0,1)
则椭圆C的一个顶点为(0,1),即b=1
由
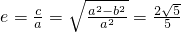 ,∴a2=5,
,∴a2=5,所以椭圆C的标准方程为

(2)证明:易求出椭圆C的右焦点F(2,0),
设A(x1,y1),B(x2,y2),M(0,y0),显然直线l的斜率存在,
设直线l的方程为y=k(x-2),代入方程
 并整理,
并整理,得(1+5k2)x2-20k2x+20k2-5=0
∴
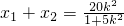 ,
,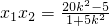
又,
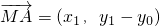 ,
, ,
,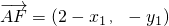 ,
,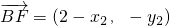 ,而
,而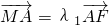 ,
,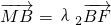 ,
,即(x1-0,y1-y0)=λ1(2-x1,-y1),(x2-0,y2-y0)=λ2(2-x2,-y2)
∴
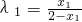 ,
,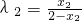 ,
,所以
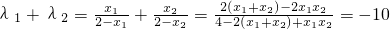
分析:(1)设出椭圆的方程,把抛物线方程整理成标准方程,求得焦点的坐标,进而求得椭圆的一个顶点,即b,利用离心率求得a和c关系进而求得a,则椭圆的方程可得.
(2)先根据椭圆的方程求得右焦点,设出A,B,M的坐标设出直线l的方程代入椭圆方程整理后利用韦达定理表示出x1+x2和x1x2,进而根据
 ,
, ,
, 和
和 利用题设条件求得λ1和λ2的表达式,进而求得λ1+λ2.
利用题设条件求得λ1和λ2的表达式,进而求得λ1+λ2.点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生综合分析问题的能力,知识的迁移能力以及运算能力.

练习册系列答案
相关题目
 已知二次函数f(x)=3x2-3x直线l1:x=2和l2:y=3tx,其中t为常数且0<<1.直线l2与函数f(x)的图象以及直线l1、l2与函数f(x)的图象围成的封闭图形如图中阴影所示,设这两个阴影区域的面积之和为S(t).
已知二次函数f(x)=3x2-3x直线l1:x=2和l2:y=3tx,其中t为常数且0<<1.直线l2与函数f(x)的图象以及直线l1、l2与函数f(x)的图象围成的封闭图形如图中阴影所示,设这两个阴影区域的面积之和为S(t). ,求证a、b、c中至少有一个等于1.
,求证a、b、c中至少有一个等于1. =(1,-2),
=(1,-2), =(a,-1),
=(a,-1), =(-b,0),a≥0,b≥0,O为坐标原点,若A、B、C三点共线,则4a+21+b的最小值是
=(-b,0),a≥0,b≥0,O为坐标原点,若A、B、C三点共线,则4a+21+b的最小值是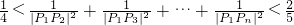 (n≥3,n∈N*).
(n≥3,n∈N*). ),β∈[0,
),β∈[0, 的取值范围是
的取值范围是 )
) ,
,