题目内容
对于下列四个命题：①
；②
；③tan138°＞tan143°；④tan40°＞sin40°．其中正确命题的序号是
- A.①③
- B.①④
- C.②③
- D.②④
B
分析：①根据正弦函数的单调性判断
②将函数化到（0，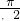
）区间上进行比较．
③根据正切函数的单调性进行比较
④根据在（0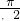，）上，tanx＞sinx比较．
解答：①f（x）=sinx在[-
，0]上为增函数，故；
②
；
③f（x）=tanx在（，π）上单调递增，故tan138°＜tan143°；
④在（0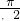，）上，tanx＞sinx，tan40°＞sin40°．故正确的为①④．
故选B．
点评：本题考查了正弦函数、余弦函数即正切函数的单调性，属于基础题型．
分析：①根据正弦函数的单调性判断
②将函数化到（0，
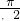）区间上进行比较．③根据正切函数的单调性进行比较
④根据在（0，
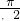）上，tanx＞sinx比较．解答：①f（x）=sinx在[-
，0]上为增函数，故；②
；③f（x）=tanx在（
，π）上单调递增，故tan138°＜tan143°；④在（0，
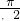）上，tanx＞sinx，tan40°＞sin40°．故正确的为①④．故选B．
点评：本题考查了正弦函数、余弦函数即正切函数的单调性，属于基础题型．
练习册系列答案
相关题目